Traitement du signal avec Scilab :
signaux aléatoires et bruits
Sommaire
3 Liaisons avec le domaine temporel
5 Annexe : programme des illustrations
_________________________________________________________________________________
Comme nous l’avons vu lors de la séance précédente, lors d’une transmission d’information, le signal reçu, qu’il soit informatif ou parasite, est un signal aléatoire.
L’objectif de cette séance est de se familiariser avec les outils d’étude des signaux aléatoires. Nous nous intéresserons plus particulièrement au cas des signaux à densité de probabilité gaussienne, qui représente la majorité des bruits en électronique que soit par exemple le bruit produit par une résistance, ou le bruit récupéré sur un canal de transmission.
1 Méthode d’étude
Un signal aléatoire est, à l’opposé d’un signal déterministe, un signal dont on ne connaît pas la loi d’évolution. Il peut être caractérisé de deux manières :
- par sa puissance et sa densité spectrale de puissance comme nous l’avons vu lors de la séance précédente,
- en terme de variable aléatoire, les valeurs potentielles du signal étant associées à une probabilité d’apparition : il est fort peu probable par exemple de retrouver une tension 10 V due au bruit thermique aux bornes d’une résistance.
Certaines propriétés statistiques du signal permettent d’établir la liaison entre les caractéristiques de la variable aléatoire et la puissance du signal comme nous allons le voir. Lors de la séance suivante, nous utiliserons un outil supplémentaire, l’auto corrélation, qui nous permettra de retrouver la densité spectrale du signal (théorème de Wiener Kintchine).
2 Etude probabiliste
La probabilité d’apparition d’une variable peut suivre plusieurs lois représentées généralement sur un graphe où on trouve en ordonnée probabilité d’apparition p(x) de la variable x qui est en abscisse.
Citons la loi de répartition uniforme, où toutes les valeurs ont même probabilité, et gaussienne avec une réponse en forme de cloche. Suivant que la variable est continue (tension due au bruit thermique aux bornes d’une résistance par exemple) ou discrète (niveau logique envoyé sur une ligne de transmission, nombre donné par un dé etc...), la réponse sera une courbe continue ou composée de raies.
La figure suivante représente, dans l’ordre, une répartition uniforme pour une variable continue, gaussienne pour une variable continue, uniforme équiprobable pour une variable discrète.
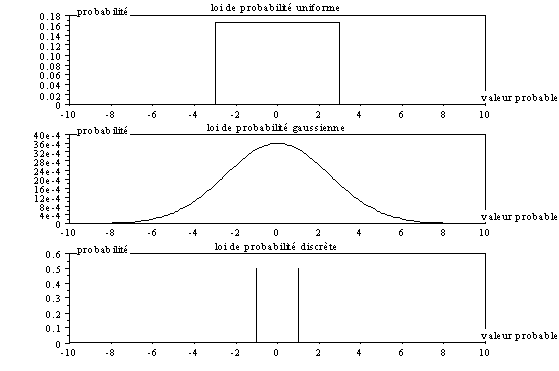
Dans le cas d’une variable discrète de N valeurs possibles, la somme des probabilités est unitaire ; de même, dans le cas d’un variable continue, la surface de la courbe est unitaire :
![]()
2.1 Loi gaussienne
Cette loi correspond à une proportion importante de phénomènes, dans des domaines aussi divers que la physique, la génétique ou la sociologie. En électronique en particulier, elle permet de caractérisé le bruit sur une ligne de transmission ou la bruit thermique d’une résistance par exemple.
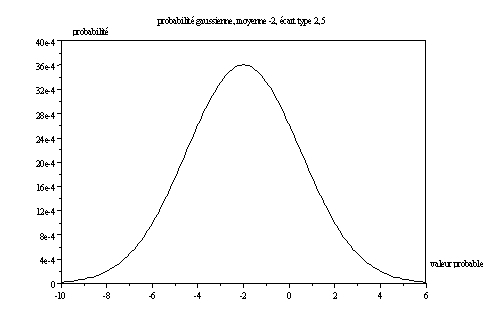
L’équation d’une telle loi de variation est donnée par :
![]()
où « m » représente l’espérance mathématique (pour notre cas de figure –2), et « s »un terme appelé « écart type ».
Le terme « m » est lié comme nous allons le
voir à la valeur moyenne du signal : de manière intuitive on comprend que
si la répartition des valeurs ci-dessus correspond à celle d’une tension électrique,
un voltmètre sensible à la valeur moyenne mesurerait la
grandeur « m ». D’après l’équation précédente, la probabilité de
« m » vaut ![]() et correspond à la
probabilité maximale.
et correspond à la
probabilité maximale.
De même, on peut remarquer que l’écart type, comme son
nom l’indique, impose une dilatation plus ou moins importante des valeurs
autour de la valeur moyenne : plus l’écart type est faible, plus les
valeurs probables sont proches de la valeur moyenne, plus il est important,
plus ces valeurs sont dispersées. Toujours en raisonnant sur une tension, on
voit de manière intuitive, qu’un signal dont l’écart type est nul est un signal
continu, tandis qu’un signal avec un écart type important présente de forte
fluctuation autour de sa valeur moyenne, et par voie de conséquence présente
une puissance normalisée fluctuante de forte valeur. D’après l’équation
précédente, nous avons ![]() .
.
3 Liaisons avec le domaine temporel
Deux propriétés importantes vont nous permettre de faire la liaison entre les caractéristiques statistique du signal et les propriétés temporelles que nous avons l’habitude d’utiliser :
- la stationnarité qui caractérise le fait que le signal observé sur n’importe quel intervalle de temps présente les mêmes propriétés statistiques,
- l’ergodicité qui établi une égalité, pour un signal stationnaire, entre propriétés statistiques et temporelles.
Dans le cas d’un signal s(t) ergodique, nous avons alors les correspondances données par le tableau suivant :
|
Propriété statistique |
Propriété temporelle équivalente |
|
Espérance mathématique ou moment d’ordre 1 :
|
Valeur moyenne ou composante continue :
|
|
Moment d’ordre 2 :
|
Puissance totale normalisée :
|
|
Variance :
|
Puissance des fluctuations :
|
|
Ecart type : s |
Valeur efficace des fluctuations :
|
On pourrait également ajouter une relation que nous verrons par la suite, qui est donnée par le théorème de Wiener-Kintchine, permettant d’obtenir la densité spectrale de puissance en calculant la transformée de Fourier de la fonction d’autocorrélation. Un des résultats fondamentaux de ce théorème est qu’un bruit dont les valeurs sont indépendantes les unes des autres présente une densité spectrale de puissance constante sur toute la bande de fréquence. Par analogie à la lumière blanche qui comprend toutes les couleurs (donc toutes les fréquences), on parle de bruit blanc. En pratique, les instruments de mesure étant limités en fréquence, on obtient que des « bruits roses ».
4 Application
Le programme ci-après permet de produire sous Scilab un signal aléatoire. On utilise pour cela la fonction rand(nl, nc,’loi’) qui génère une matrice de nl lignes sur nc colonnes de variables aléatoires.
Si on impose une loi normale (c’est à dire gaussienne) à l’aide de « loi=n », les variables sont comprises entre –1 et 1 avec une répartition centrée (sur 0) gaussienne d’écart type unitaire.
Si on impose une loi uniforme (« loi=u »), les variables sont comprises entre 0 et 1 avec une équiprobabilité d’apparition.
Le programme permet de choisir la loi de variation, normale ou uniforme et de visualiser l’histogramme des valeurs.
Dans le cas d’une loi normale, on peut imposer la valeur moyenne (Vmoy) et la variance (p). Attention, ces paramètres n’ont pas de signification particulière dans le cas d’une loi normale.
Toujours dans le cas d’une loi normale, la courbe de probabilité théorique est tracée avec l’histogramme. On pourra alors constater l’importance du nombre d’échantillons (paramètres N) pour que la pratique vérifie la théorie.
Enfin on calcule la densité de puissance, grâce à laquelle nous pourrons vérifier que nous avons affaire à un bruit blanc. L’expression utilisée est celle des signaux échantillonnés, les seules valeurs connues étant en effet celles données par la fonction « rand ».
La puissance est calculée de deux manières, par la variable temporelle et par la DSP (suite à la remarque précédente, il faudra cette fois diviser la sommation par le nombre N d’échantillons). On pourra vérifier la correspondance avec la variance dans le cas d’une variable gaussienne.
clear
//
// définition des constantes
loi='n';N=4096; V_moy=2; p=.5; x=(-6:.1:6);
//
// génération du bruit
bruit=sqrt(p)*rand(1,N,loi)+V_moy;
//
// calcul de la DSP
dsp=1/N*(abs(fft(bruit,-1)))^2 ;
//
// courbe théorique de probabilité
p_g=1/(sqrt(p)*sqrt(2*%pi))*exp(-((x-V_moy)^2)/2/p);
//
// affichage
xset("window",0) ; xbasc(0); xset("font
size",4);
xsetech([ 0, 0, 1,
1/3]) ; plot2d(bruit) ;
xtitle("signal
temporel"," temps (s)" ,"amplitude (V)") ;
//
xsetech([ 0, 1/3, 1,
1/3]) ;
histplot(x,bruit) ; plot2d(x,p_g) ;
xtitle("loi de probabilité théorique et histogramme" ,"
valeur probable" ,"probabilité") ;
//
xsetech([ 0, 2/3, 1, 1/3]); plot2d(10*log10(abs(dsp)))
xtitle("densité spectrale de puissance","fréquence"," DSP") ;
//
// calcul des puissances
puissance_f=1/N*sum(dsp)
puissance_t=1/N*sum(bruit^2)
Voici les résultats obtenus avec une valeur moyenne nulle et une puissance fluctuantes de 3 V2.

Le chronogramme est bien celui d’un signal à valeur moyenne nulle, et on peut estimer grossièrement la valeur efficace aux alentours de 2 V (valeur réelle 1,732 V).
L’histogramme suit bien la courbe gaussienne théorique, en étant centré autour de 0 et d’un écart type estimable à environ 2 (il se lit lorsque la variable prend une probabilité correspondant à la probabilité maximale multipliée par 0,6, soit un écart type théorique de 1,732 dans notre cas).
La densité spectrale de puissance est constante : les valeurs étant purement aléatoires, aucune fréquence n’est favorisée. On peut donc déduire que la DSP vaut 3 V2 . FE, le terme FE étant la fréquence d’échantillonnage et valant 1 dans notre cas, ce qui donne une DSP de 3, soit 4,7 dB. La fluctuation importante autour de la valeur nous interdit toute lecture précise, mais cette valeur n’est pas incompatible avec le graphique. Pour plus de précision, la DSP pourrait être calculée avec la fonction « pspect » que nous utiliserons lors de la prochaine séance.
La puissance calculée par les méthodes temporelle et fréquentielle, donne une valeur de 2,96 V2, ce qui correspond bien au résultat attendu à 2% (le nombre d’échantillons n’étant pas infini, la répartition n’est pas exactement gaussienne, comme le montre la différence entre l’histogramme et la courbe théorique).
Voici maintenant les résultats avec une valeur moyenne de 2 V et une puissance fluctuante de 0,5 V2.
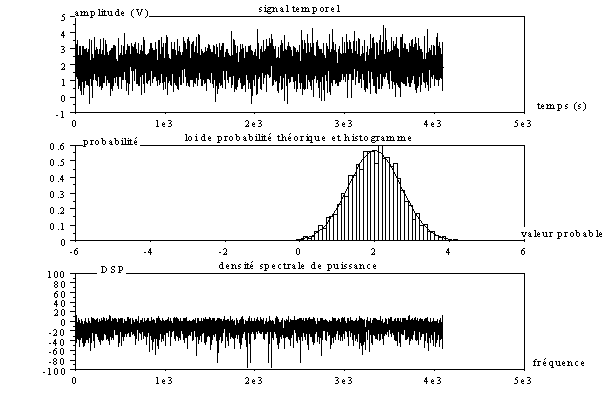
Analyser les courbes comme précédemment et justifier les valeurs (attention, la DSP présente une raie à la fréquence nulle). Noter l’évolution de la gaussienne. Le calcul de la puissance donne 4,456 V2.
Bibliographie
Principes fondamentaux des télécommunications par P.Clerc et P.Xavier chez Ellipse
Transmission de signaux par C. More chez Tec & Doc
5 Annexe : programme des illustrations
Différentes lois de probabilité
clear;
//
// définition
des constantes et variable d’ordonnées
mx=10 ;
pas=0.1 ;
x=(-mx : pas :
mx);
m=0 ; sig=2.5 ;
//
// variable
gaussienne
p_g=1/(sig*sqrt(2*%pi)*exp(-((x-m)^2)/2/sig^2));
//
// variable uniforme
n=6 ;
p_u=1/n*[zeros(1,(mx-n/2)), ones(1,n), zeros(1,
(mx-n/2))] ;
//
// variable discrète
nb=2 ;
p_disc=1/nb*[zeros(1,9), 1, 0, 1, zeros(1, 8)] ;
//
// affichage
xset("window",0) ; xbasc(0); xset("font
size",4);
xsetech([ 0, 1/3, 1, 1/3]) ; ;
plot2d(x,p_g)
xtitle("loi de probabilité gaussienne"," valeur
probable" ,"probabilité") ;
//
xsetech([ 0, 0, 1,
1/3]) ; plot2d2((-mx :mx-1),p_u)
;;
xtitle("loi de probabilité uniforme" ," valeur
probable" ,"probabilité") ;
//
xsetech([ 0, 2/3, 1, 1/3]) ; ;
plot2d3((-mx :mx-1),p_disc, rect=[-mx, 0, mx, 1.2/nb])
xtitle("loi de probabilité discrète"," valeur
probable" ,"probabilité") ;
Probabilité gaussienne
clear;
m=-2 ; sig=2.5 ;
x=-10: .1 :6;
p=1/(sig*sqrt(2*%pi)*exp(-((x-m)^2)/2/sig^2));
xset("window",0)
; xbasc(0); xset("font size",4);
plot2d(x,p) ;
xtitle(" probabilité gaussienne, moyenne -2, écart type
2,5"," valeur probable" ,"probabilité" );