Traitement du signal avec Scilab : Signaux échantillonnés
Sommaire
5 Théorème de l'échantillonnage
___________________________________________________________________
Le passage de l’analogique au numérique passe par l’opération d’échantillonnage, dont la compréhension est nécessaire à l’étude des systèmes numériques. Au cours de cette séance, nous allons étudier dans le domaine temporel et fréquentiel les propriétés et conséquences de cette opération. Un système de modulation d'impulsion en amplitude sur réseau téléphonique servira de support à notre étude. Ce système étant purement analogique, on s’affranchit ainsi de l’opération de quantification.
1 Description du système
Cette étude s'inspire d'un réseau téléphonique local privé, nommé Jistel. Afin de pouvoir transmettre plusieurs conversations sur la ligne unique du réseau, les signaux issus des différents postes téléphoniques sont échantillonnés à une fréquence Fe = 16 kHz (soit une période de Te = 62,5 µs) et les impulsions transmises par multiplexage temporel : chaque impulsion occupe un intervalle de temps de 976 ns sur une période de 62,5 µs. Il est alors possible de transmettre 64 signaux sur la ligne soit 32 conversations simultanées.
L'échantillonnage de la tension ve représentant le signal informatif revient à considérer que celle-ci est multipliée par un train d'impulsions de courte durée, d’amplitude unitaire et de période TE.
Par la suite nous approfondirons cette notion en considérant des impulsions de Dirac de largeur t et d'amplitude 1/t s-1 (la valeur de t tendant vers zéro).
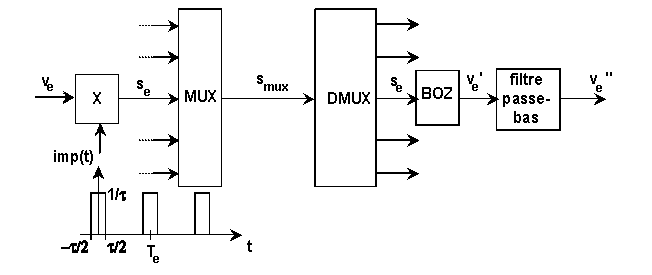
Les signaux arrivant des différents postes téléphoniques subissent alors un multiplexage temporel avant d'être redistribués vers le bon récepteur par le système de démultiplexage. Pour retrouver la tension d'origine ve il faut passer le signal se dans un bloqueur d'ordre 0. Celui-ci convertit la suite d'impulsions en un signal en "marches d'escalier" dont la valeur sur une période Te est égale à l'amplitude de l'impulsion d'entrée se au début de cette période. Afin de lisser le signal (supprimer les marches d’escalier), on lui fait subir un filtrage passe bas en sortie duquel la tension ve'' est théoriquement identique à ve.
2 Etude générale
Nous allons dans un premier temps nous intéresser à la représentation temporelle des signaux. La principale difficulté sera d’éviter la confusion entre la fréquence d’échantillonnage à 16 kHz du système étudié, et la fréquence, que nous appellerons de calcul, nécessaire pour effectuer notre simulation.
Le programme suivant définit dans un premier temps les différentes constantes. Cette étape nous laissera la possibilité de modifications ultérieures de ces paramètres.
Les différentes opérations sont ensuite effectuées.
Le blocage et le filtrage sont réalisés par produit de convolution avec la réponse impulsionnelle du quadripôle concerné, bien que nous ayons vu que cette opération effectuait sous Scilab par un produit de transformée de Fourier. De cette manière, l’aspect fréquentielle reste pour nous presque transparent.
La réponse impulsionnelle du bloqueur est une simple fonction porte d’amplitude unitaire et de largeur Te.
Pour déterminer celle du filtre, nous utilisons la fonction « analpf » afin de déterminer la fonction de transfert d’un filtre de Butterworth du 8ème ordre, de fréquence de coupure 0,4.Fe. La fonction « freq » permet ensuite de calculer les différentes valeurs numériques, puis avant de calculer la réponse impulsionnelle par transformée de Fourier inverse, on remet en forme la fonction de transfert afin de respecter les symétries de la transformée de Fourier d’un signal réel (revoir la première séance sur la modulation BLU).
clear
//
// définition des constantes, nombre de points par périodes de dirac, largeur du dirac, nombre de diracs, nombre de points total, fréquence et temps de calcul,
// fréquence et période du peigne de dirac et fréquence du signal
Npp=40 ; a=1; Nd=80; N=Npp*Nd;
Fe=16e3; Te=1/Fe; Fc=Fe*Npp; Tc=1/Fc; F=1000;
//
// description du vecteur temps
t=Tc*(0:N-1);
//
// signal à échantillonner
ve=5*sin(2*%pi*F*t);
//
// une période du dirac de rapport cyclique a/Npp
d=[ones(1, a), zeros(1, (Npp-a))];
//
// peigne de dirac sur Nd périodes
imp=matrix(d' *ones(1, Nd ), 1 , N);
//
// signal échantillonné
se=ve .* imp;
//
// réponse impulsionnelle du bloqueur
b=ones(1, Npp);
//
// signal en sortie du bloqueur, réajusté sur N points
v1= convol(b,se);
v1=v1(1 : N);
G=analpf(8,'butt',[0 0],2*%pi*(0.4*Fe));
f=Fc/N*[0 : N-1];
GAIN=freq(G(2),G(3),%i*2*%pi*f);
G=[GAIN(1:N/2),
conj(GAIN(N/2+1:-1:2))];
hpb=fft(G, 1);
//
// filtrage
v2=convol(hpb, v1); v2=v2(1:N);
// affichage
xset("window",0); xbasc(0) ;
xset(“font size”,4);
xsetech([0,0,1,1/4]) ; plot2d(t,ve); plot2d2(t,imp);
xtitle(“signal entré, peigne de Dirac”,”temps (s)”,”amplitude (V)”)
xsetech([0,1/4,1,1/4]) ; plot2d2(t,se);
xtitle(“signal échantillonné”,”temps (s)”,”amplitude (V)”);
xsetech([0,2/4,1,1/4]) ;
plot2d2(t,v1);
xtitle(“signal bloqué”,”temps (s)”,”amplitude (V)”)
xsetech([0,3/4,1,1/4]) ;
plot2d2(t,v2);
xtitle(“signal de sortie filtré”,”temps (s)”,”amplitude (V)”);
Voici les courbes affichées pour un signal sinusoïdal en entrée, de fréquence 1 kHz et d’amplitude 5 V. On obtient bien les résultats attendus. On constate simplement sur le signal de sortie un retard d’une période d’échantillonnage à laquelle vient s’ajouter le temps de propagation du filtre.
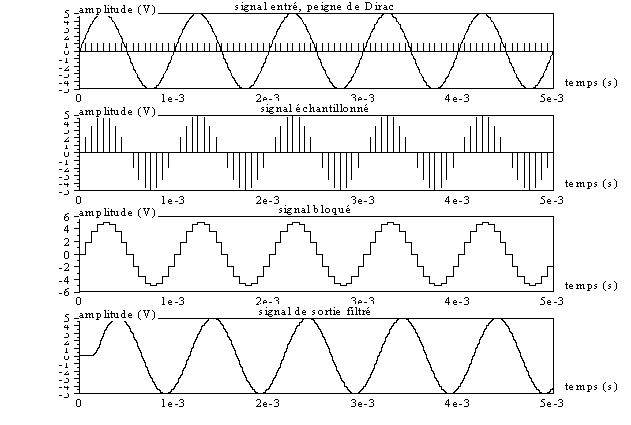
Voici maintenant ces courbes pour une fréquence de 4 kHz en entrée (et Nd=20). On peut remarquer que le signal de sortie est atténué (au zoom, environ 4,5 au lieu de 5 d’amplitude crête), atténuation que ne peut justifier seul le filtre, car à cette fréquence son gain est presque unitaire (avec Nd=20, la fréquence de 4 kHz se trouve à l’indice 6 et « abs(GAIN(6)) » donne 0,9997291).
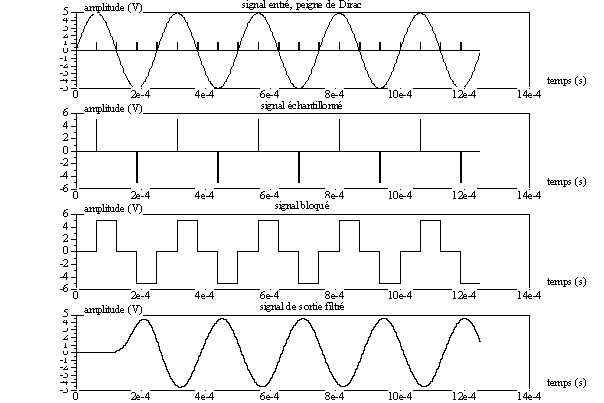
Les figures suivantes mettent en évidence le phénomène du sous échantillonnage avec une fréquence d’entrée cette fois de 12kHz.
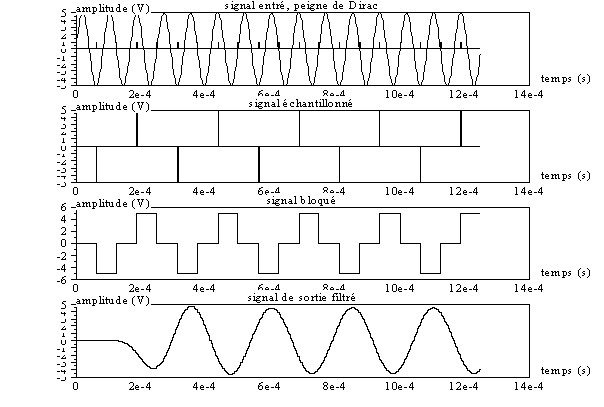
On constate une fréquence de sortie de 4 kHz.
3 Etude du modulateur
a) Donner en fonction de imp(t) et de ve(t), l'expression de se(t).
b) Même question dans le domaine fréquentiel avec IMP(jw), VE(jw) et SE(jw).
c) Nous allons maintenant considérer le signal imp(t) comme une suite d’impulsions de largeur t et de hauteur 1/t, (voir la première figure).Cette représentation nous permettra de calculer le spectre des impulsions idéales (de largeur nulle et d'amplitude unitaire), sans faire appel à la théorie des distributions.
Remarque importante
Le signal se issu du multiplicateur a donc pour unité en utilisant ce formalisme des Vs-1. Historiquement, l'échantillonnage et le traitement des signaux se sont dans un premier temps fait à l'aide de systèmes analogique, dans lesquels les grandeurs en transit avait une unité bien définie (des volts par exemple).
L'étude des signaux demandait alors une certaine rigueur afin de conserver l'homogénéité des expressions obtenues, le principal problème consistant à donner une énergie à une grandeur qui dans le cas idéal était une suite d'impulsions de durée nulle.
La solution mathématique à ce problème à été apportée par la théorie des distributions.
L'utilisation aujourd'hui largement répandue de calculateurs numériques (processeurs de signaux et autres) transforme un signal en une suite de nombres où le problème énergétique est beaucoup moins important, ce qui autorise un certain nombre de raccourcis et abus de langage.
Afin de ne pas alourdir cet exercice, nous nous autoriserons également ces libertés, la première apparaissant avec la définition du signal imp(t) donné lors de la description du système, où l'amplitude est exprimée en secondes. Sans cet artifice, le signal disparaît lorsque t tend vers 0, et il devient difficile alors d'étudier le système dans le cas d'un échantillonnage idéal.
Décomposer en série de Fourier de termes réels le signal imp(t) pour une valeur quelconque de t. et mettre cette expression sous forme d'un sinus cardinal (sincx = (sinx)/x dont l'évolution est donnée en annexe).
Vérifier le calcul en montrant que si t=TE/2 on retrouve bien la décomposition en série de Fourier d'un signal carré. On rappelle que pour un signal s(t) carré d'amplitude +/-A (soit 2A crête à crête), on obtient par décomposition en série de Fourier les coefficients :
![]()
Représenter le spectre d'amplitude du signal dans le cas particulier suivant :
![]()
Pour cela, on remarquera que le spectre obtenu est un spectre de raies, contenues dans une enveloppe dont l'équation est connue. On tracera donc en premier lieu l'enveloppe du spectre avant de placer les raies.
Faire tendre t vers zéro dans l'expression des termes de la série . Représenter le nouveau spectre d'amplitude.
d) Calculer la décomposition de Fourier en termes complexes de imp(t). Vérifier la correspondance des deux spectres.
Vérifions ces calculs par la simulation. Le programme suivant permet de calculer et d'afficher le spectre pour différents rapports cycliques, imposés par le paramètre « a ». L’amplitude du signal carré 1/t dans le cas du programme vaut alors Npp/(a.Te) ; on vérifie bien avec ce formalisme que si a=Npp, on a bien t=Te.
On a également effectué le calcul de l’enveloppe en sinus cardinal du spectre. Celle-ci est affichée avec des pointillés, pour un point sur 4. Ce calcul pose le problème de l’indétermination au point f=0, où le dénominateur du sinus cardinal est nul. La solution est donné par la fonction « == » qui précise une condition et non une affectation ; le fonctionnement est le même qu’en langage C : si la condition « f nul » est vérifiée, la fonction « == » renvoie le nombre 1, et 0 dans les autres cas.
clear ;
// rappel des paramètres, redéfinition de l’amplitude de imp
Npp=40 ; a=20; Nd=20; N=Npp*Nd;
Fe=16e3; Te=1/Fe; Fc=Fe*Npp; Tc=1/Fc;
// description du vecteur temps
t=Tc*(0:N-1);
//
// une période du dirac de rapport cyclique a/Npp
d=[ones(1, a), zeros(1, (Npp-a))];
//
// peigne de dirac d’amplitude 1/a sur Nd périodes
tau=a*Te/Npp ;
imp=1/tau*matrix(d' *ones(1, Nd ), 1 , N);
//
// analyse de Fourier
f=Fc/N*[0:N/2-1];
IMP=1/N*abs(fft(imp,-1));
IMP=IMP(1:N/2);
//
// génération du sinus cardinal
S=abs(Fe*(sin(tau*%pi*f)./((tau*%pi*f+(f==0))) +(f==0))) ;
//
// affichage
xset("window",0); xbasc(0) ;
xset(“font size”,6);
xsetech([0,0,1,1/2]) ; plot2d2(t,imp, rect=([0, 0, 14E-4, 1.2*Npp/(a*Te)]) );
xtitle(“signal en fonction du temps”,”temps (s)”,”amplitude”)
xsetech([0,1/2,1,1/2]) ;
plot2d(f,IMP, rect=([0,
0, 32e4, 1.2*Fe]));
plot2d(f(1 :4 :length(f)),S(1 :4 :length(f)),
style=-3, rect=([0, 0, 32e4, 1.2*Fe]));
xtitle(“signal en fonction de la fréquence”,”fréquence (Hz) ”,”amplitude”);
Voici l’affichage pour un signal carré (a=20) :
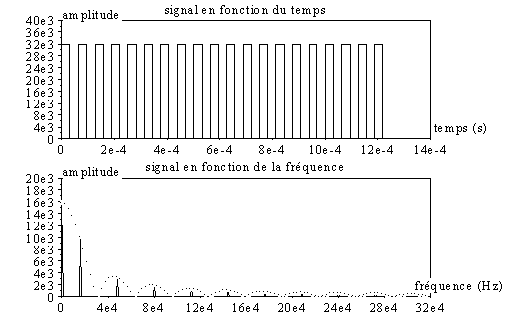
On constate que les raies sont bien comprises dans l’enveloppe du sinus cardinal. On note également pour cette valeur particulière du rapport cyclique la décroissance en 1/n (n étant le rang de la fréquence harmonique par rapport à la fondamentale) des amplitudes.
Voici maintenant le spectre pour a égale 6 ( pour t=TE/6 il faut a=6,66) :
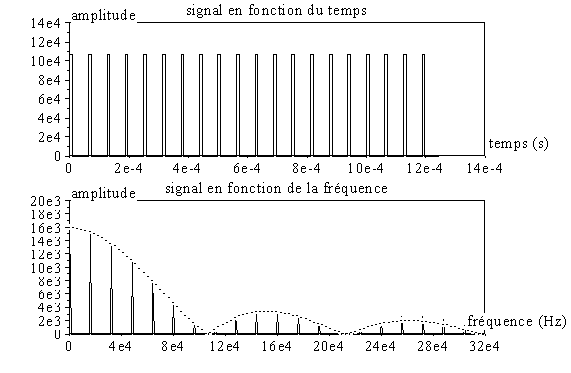
Les lobes du sinus cardinal se sont élargis (t a changé de valeur) et on retrouve plus de raies dans chaque lobe.
On constate également un dépassement de plus en plus important de l’enveloppe théorique au fur et à mesure que la fréquence augmente :
- comme nous l’avons déjà signalé dans notre approche qualitative des signaux, échantillonner un signal revient à périodiser son spectre ; nous avons en effet une multiplication dans le domaine temporel par un peigne de Dirac, donc une convolution dans le domaine fréquentiel par un peigne de Dirac (fréquentiel cette fois). Comme nous l’avons vu lors de la première séance sur Scilab, notre calculateur étant numérique, il échantillonne donc les signaux, tous les spectres qu’il calcule sont donc périodiques, même si dans notre cas nous n’en visualisons qu’un partie. L’accroissement des raies que nous observons pour les hautes fréquences est en fait un repliement de spectre : les raies autour de la fréquence d’échantillonnage (Fc dans notre cas) se superposant aux raies autour de 0. Voici la spectre que donnerait le programme si on ne limitait pas la fréquence à Fc/2.

- Cette notion sera revue lors de la prochaine séance lors de la transformation de Fourier discrète.
- Si nous n’avons pas observé ce phénomène avec un rapport cyclique 0,5, c’est tout simplement parce que la décroissance des harmoniques est plus rapide dans ce cas (une observation attentive met cependant le phénomène en évidence).
Enfin pour la plus petite valeur possible avec notre programme, soit a=1 :
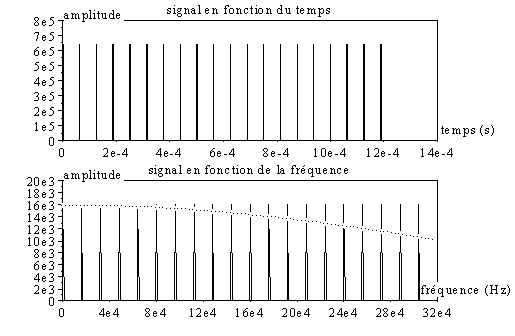
Dans ce dernier exemple, on ne devrait pas trouver des raies d’amplitude constante, car nous n’avons pas réellement t=0 ; cependant, le repliement de spectre nous donne l’illusion d’une suite temporelle d’impulsion de durée nulle.
e) Déduire de la question a), la représentation graphique du spectre d'amplitude bilatéral de SE (on écrira pour cela le signal ve(t) sous sa forme exponentielle).
Le programme ci-après (écrit à la suite du précédent), permet de tracer le spectre du signal échantillonné.
// signal à échantillonner
F=3000 ; ve=5*sin(2*%pi*F*t);
//
// signal échantillonné
se=ve .* imp;
VE=1/N*abs(fft(ve,-1));
VE=VE(1:N/2);
//
SE=1/N*abs(fft(se,-1));
SE=SE(1:N/2);
//
// affichage
xset("window",1); xbasc(1) ;
xset(“font size”,4);
xsetech([0,0,1,1/3]) ;
plot2d(f, VE );
xtitle(“signal en entrée”,”fréquence”,”amplitude”)
xsetech([0,1/3,1,1/3]) ;
plot2d(f, IMP );
xtitle(“impulsions”,”fréquence”,”amplitude”)
xsetech([0,2/3,1,1/3]) ;
plot2d(f, SE);
xtitle(“signal échantillonné”,”fréquence”,”amplitude”);
Pour tracer la figure, on a imposé une fréquence d’entrée de 3 kHz et a=6 ; d’autre part, afin d’obtenir un pas d’affichage de 1 kHz (le pas d’affichage donné par la fonction « fft » est Fc/N=Fe/Ndd –revoir la première séance-), le paramètre Ndd est fixé à 16. Cette notion sera détaillée lors de la prochaine séance sur la transformée de Fourier discrète.
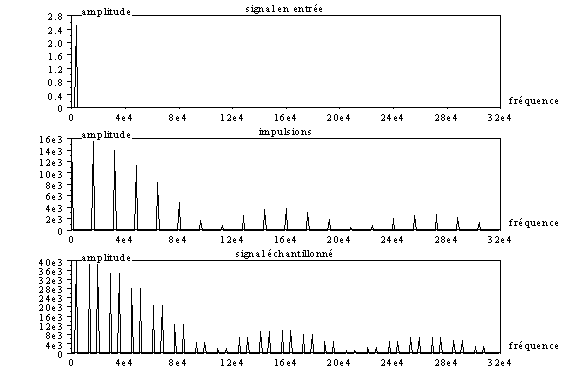
On notera sur cette figure, le résultat d’un produit de convolution entre deux spectres de raies.
f) La théorie des distributions nous définit l'impulsion de Dirac comme une impulsion d'amplitude unitaire pour t=0 et nulle partout ailleurs :
d(t)=1 pour t=0
d(t)=0 pour t 0
On appelle "peigne de Dirac" la suite d'impulsions de Dirac espacées de TE et notée PgnTE.
Donner l'expression mathématique (sous forme d'une sommation) de PgnTE.
Si on considère que l'amplitude unitaire d'une impulsion de Dirac représente la surface de cette impulsion, on remarquera que dans le cas idéal (t=0), imp(t) et PgnTE sont identiques.
On note {se(nTE)} la suite de valeurs obtenues à partir de l'échantillonnage de ve(t) aux instants nTE.
Donner alors l'expression mathématique de {se(nTE)} en fonction de ve(t) et d(t) dans le cas d'un échantillonnage idéal.
Remarques :
Dans la littérature, on note souvent s*(t) le signal résultant de l'échantillonnage de s(t) ;
la suite {s(nTE)}, notée aussi {s(n)}, représente la suite de nombres (version numérique du signal échantillonné) obtenue à partir de la numérisation de s*(t) (qui est la version analogique du signal échantillonné).
L'expression s(nTe) ou s(n) représente quant à elle la valeur particulière numérisée à l'instant nTE de s(t).
Par abus d'écriture, les expressions {s(n)} et s(n) sont souvent confondues.
Bien que notre système présente juste un échantillonnage et pas de quantification (ou numérisation), nous avons malgré tout utilisé la notation {s(nTE)}.
En vous inspirant des expressions précédentes, donner l'expression mathématique du spectre du signal échantillonné se (dans le cas d'un échantillonnage idéal).
4 Etude du démodulateur
a) Représenter en fonction du temps la réponse impulsionnelle du bloqueur d'ordre 0.
Déterminer alors la réponse fréquentielle du bloqueur par deux méthodes :
- en effectuant le calcul de l’intégrale de Fourier à partir de la réponse impulsionnelle ;
- en remarquant que la réponse impulsionnelle est la somme de deux échelons dont un est retardé (la réponse fréquentielle d'un échelon unité est 1/jw)
Mettre le module sous la forme TE sinc(wTE/2) et représenter graphiquement son évolution en fonction de la fréquence (échelles linéaires).
b) Déduire de la question précédente la représentation graphique du spectre d'amplitude de la tension ve' (dans le cas où t tend vers 0).
Le programme suivant permet d’effectuer une simulation dans le cas où le signal d’entrée est la somme de deux sinusoïdes, d’amplitude 5 V et de fréquences 2 et 4 kHz.
Le coefficient « z » qui intervient dans la définition du vecteur fréquence permet d’obtenir un effet « zoom » sur l’affichage du spectre fréquentiel.
Notons également la valeur de « Nd » passée à 160 et le coefficient de 1/100 pour le calcul de la réponse fréquentielle du bloqueur :
- comme nous l’avons déjà remarqué lors de la première séance (voir l’annexe sur les fonctions), les valeurs spectrales que nous donne Scilab sont discrètes (par pas de Fc/N=Fe/Nd soit 100 Hz dans notre cas). Le spectre est donc composé de raies (même si des artifices d’affichage nous permettent de donner l’illusion qu’il est continu) et par voie de conséquences, le signal temporel est considéré comme périodique, de période correspondant à la fenêtre de visualisation (où moins s’il y a une vraie périodicité qui apparaît lors de l’acquisition), soit N.Tc dans notre cas. Pour obtenir les amplitudes exactes des raies, il faut donc faire une égalité entre ce que donnerait la décomposition en série de Fourier du signal périodique, et ce que donnerait la transformée de Fourier du signal vu sur une seule période (même si les unités sont différentes). Le calcul sur une seule raie suffit, la composante continue étant la plus simple à déterminer. Dans notre exemple, il s’agit d’un signal impulsionnel, qui vu comme un signal périodique de période N.Tc a une composante continue de Te/(N.Tc) soit en fonction des diverses relations 1/Nd. Les calculs de la transformée de Fourier nous donnent une amplitude en continu de Te. On doit donc vérifier Nd Te=1, soit Nd=16 000. Cette valeur élevée (16 000 périodes de Npp points chacune), conduirait à des temps de calculs important et surtout la difficulté par le logiciel de gérer certaines fonctions comme l’affichage. Aussi avons nous préféré garder un nombre Nd de 160 plus raisonnable (pas d’affichage de 100 Hz) et tricher sur le calcul de la réponse fréquentielle du bloqueur en introduisant un coefficient de 1/100.
- Toutes ces notions seront détaillées lors de la séance suivante sur la transformée de Fourier discrète.
clear ;
// rappel des paramètres
Npp=40 ; a=1; Nd=160; N=Npp*Nd; Fe=16e3; Te=1/Fe; Fc=Fe*Npp; Tc=1/Fc;
//
// description du vecteur temps et fréquence avec un « zoom » pour la fréquence
t=Tc*(0:N-1);
z=10 ; f=Fc/N*[0:N/z-1];
//
// peigne de dirac d’amplitude 1/a sur Nd périodes
tau=a*Te/Npp ;
d=[1*ones(1, a), zeros(1,
(Npp-a))]; imp=1/tau*matrix(d' *ones(1, Nd ), 1 , N);
//
// signal à échantillonner et échantillonnage
F1=2000 ;F2=4000 ; ve=5*(sin(2*%pi*F1*t)+sin(2*%pi*F2*t));
se=ve .* imp;
//
// réponse impulsionnelle du bloqueur
b=ones(1, Npp); b2=[b, zeros(1,N-Npp)];
//
// analyse de Fourier
IMP=1/N*abs(fft(imp,-1)); IMP=IMP(1:N/z);
VE=1/N*abs(fft(ve,-1)); VE=VE(1:N/z);
SE=1/N*abs(fft(se,-1)); SE=SE(1:N/z);
B=1/N*abs(fft(b2,-1)); B=0.01*B(1 :N/z) ;
V1=SE.*B ;
//
// affichage
xset("window",0); xbasc(0) ;
xset(“font size”,4);
xsetech([0,0,1,1/3]) ;
plot2d(f, SE, rect=[0,
0, 7e4, 1.2*Fe*2.5] );
xtitle(“spectre du signal en entrée”,”fréquence”,”amplitude”)
xsetech([0,1/3,1,1/3]) ;
plot2d(f, B );
xtitle(“réponse fréquentielle du bloqueur”,”fréquence”,”amplitude”)
xsetech([0,2/3,1,1/3]) ;
plot2d(f, V1);
xtitle(“spectre du signal en sortie du bloqueur”,”fréquence”,”amplitude”);
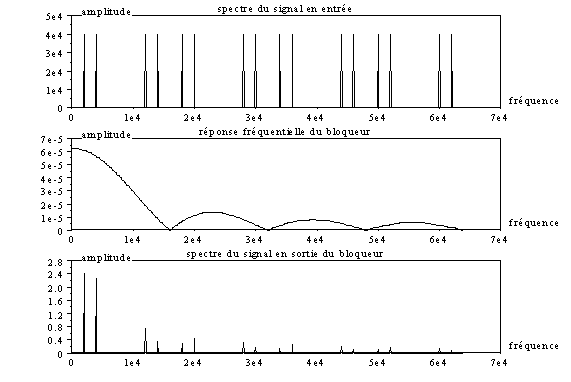
Le bloqueur atténue fortement les harmoniques hautes fréquences autour des multiples de la fréquence d’échantillonnage. Ceux-ci ne sont cependant pas complètement supprimés, ce qui explique les marches d’escalier sur la représentation temporelle du signal v’e, et justifie la présence d’un filtre.
On peut maintenant également expliquer ce que nous avions constaté lors de l’étude temporelle, en particulier avec le signal d’entrée à 4 kHz : même dans la bande utile, les signaux de fréquences les plus élevées sont atténués par le bloqueur (comparer les raies à 2 et 4 kHz).
c) Afin de retrouver les informations contenues dans ve, quel doit être le spectre d'amplitude de VE'' (on négligera les variations de phase auxquelles l'oreille humaine est peu sensible).
Remarque : le filtre que nous avons choisi avec une bande passante de 6,4 kHz répond largement aux exigence des normes téléphoniques où la bande du signal utile est 300 Hz – 3400 Hz. Ce choix nous a permis de mettre en évidence, dès l’étude temporelle, l’atténuation due au bloqueur.
Voici maintenant les dernières instructions à ajouter au programme précédent afin de représenter l’ensemble des spectres des signaux (pour z=15) :
// calcul du
filtre et filtrage
G=analpf(8,'butt',[0 0],2*%pi*(0.4*Fe));
GAIN=freq(G(2),G(3),%i*2*%pi*f);
V2=GAIN.*V1 ;
//
// affichage
xset("window",1); xbasc(1) ;
xset(“font size”,4);
xsetech([0,0,1,1/6]) ;
plot2d(f, VE, rect=[0,
0, 4e4, 5] );
xtitle(“spectre du signal en entrée”,”fréquence”,”amplitude”)
xsetech([0,1/5,1,1/6]) ;
plot2d(f, SE, rect=[0,
0, 4e4, 1.2*Fe*2.5] );
xtitle(“signal modulé”,”fréquence”,”amplitude”)
xsetech([0,2/5,1,1/6]) ;
plot2d(f, abs(V1) ,
rect=[0, 0, 4e4, 5]);
xtitle(“spectre du signal en sortie du bloqueur”,”fréquence”,”amplitude”);
xsetech([0,3/5,1,1/6]) ;
plot2d(f, abs(GAIN ) ,
rect=[0, 0, 4e4, 1.1]);
xtitle(“réponse fréquentielle du filtre”,”fréquence”,”amplitude”)
xsetech([0,4/5,1,1/6]) ;
plot2d(f, abs(V2), rect=[0,
0, 4e4, 5] );
xtitle(“spectre du signal restitué”,”fréquence”,”amplitude”)
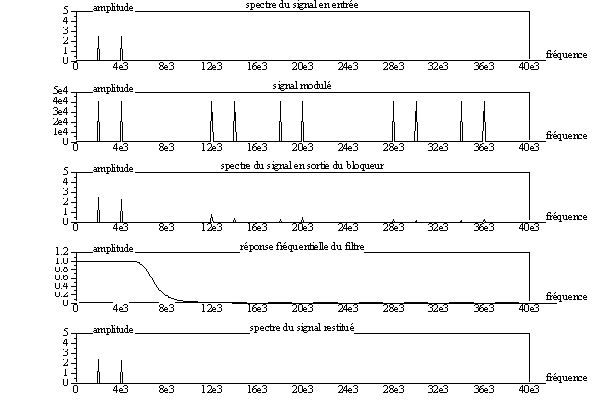
5 Théorème de l'échantillonnage
a) D'après ce qui précède, déterminer la valeur minimale de FE qui permettrait théoriquement de restituer le signal ve en ve''.
Justifier la présence d’un signal 4 kHz en sortie lorsque le signal d’entrée est de 12 kHz (voir figures de l'étude temporelle).
Voici le résultat de la simulation dans ce cas particulier :
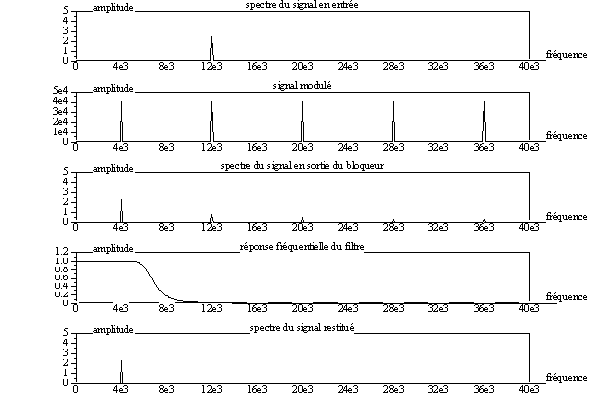
b) Généraliser sur le choix d'une fréquence d'échantillonnage par rapport à la fréquence maximale du signal à échantillonner (théorème de Shannon).
Annexe 1 : le sinus cardinal
Nous le définissons comme ![]() , mais certaines définitions utilisent :
, mais certaines définitions utilisent : ![]() .
.
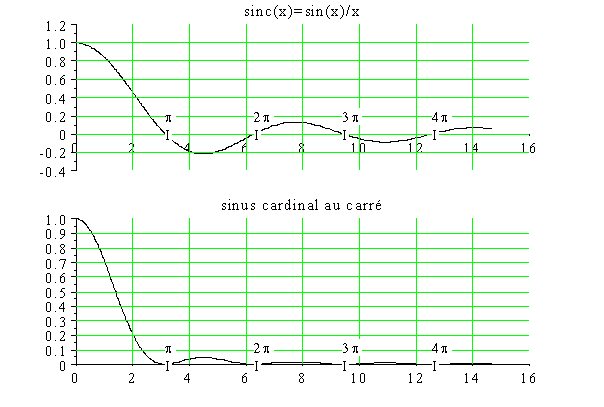
Ces courbes sont générées par le programme suivant :
clear ;
Delta=0.01 ; N=5*%pi ;
x=(0:Delta :N-1);
//
// génération du sinus cardinal
S=sin(x)./((x+(x==0))) +(x==0) ;
//
// affichage du sinus cardinal
xset("window",0); xbasc(0) ;
xset(“font size”,6);
xsetech([0,0,1,1/2]) ;
plot2d(x,S,
axesflag=[5]);
xtitle(“sinc(x)=sin(x)/x”,””,””); xgrid(3);
// affichage des graduations multiples de p
xset("font", 1, 12);
xstring( %pi, 0.1,["p"]); xstring(
2*%pi, 0.1,["2p"]); xstring( 3*%pi, 0.1,["3p"]); xstring(
4*%pi, 0.1,["4p"]);
xset("font",2, 18);
xstring(%pi, -0.12,["I"]);
xstring(2*%pi, -0.12,["I"]); xstring(3*%pi, -0.12,["I"]);
xstring(4*%pi, -0.12,["I"]);
//
// affichage du sinus cardinal carré
xsetech([0,1/2,1,1/2]) ;
plot2d(x, S^2,
axesflag=[5]);
xtitle(“sinus cardinal au carré”,””,””); xgrid(3);
xset("font", 1, 12);
xstring(%pi,0.05,["p"]);
xstring(2*%pi,0.05,["2p"]); xstring(3*%pi,0.05,["3p"]);
xstring(4*%pi,0.05,["4p"]);
xset("font",2, 18);
xstring(%pi, -0.08,["I"]);
xstring(2*%pi, -0.08,["I"]); xstring(3*%pi, -0.08,["I"]); xstring(4*%pi,
-0.08,["I"]);