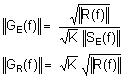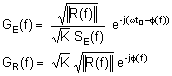Traitement du signal avec Scilab :
transmission numérique en bande de base
Sommaire
1. Cas d’un canal non bruité de bande passante réduite
1.4. Suppression de
l’interférence entre symbole
2. Cas d’un canal bruité de bande passante infinie
___________________________________________________________________
La transmission d’informations numériques en bande de base, même si elle peut paraître simple au premier abord, nécessite un certain nombre de précautions si on souhaite obtenir des performances acceptables.
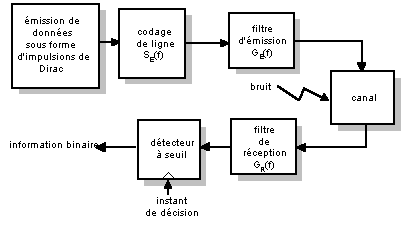
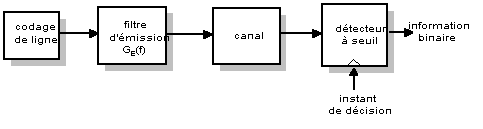
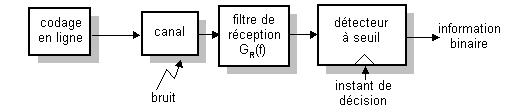
Le schéma synoptique de base d’une telle transmission est représenté par la figure suivante :

Après un codage dit de source de l’information où une compression est effectuée afin de limiter le débit (code MPEG pour les signaux vidéo par exemple), un second codage permet cette fois d’introduire une redondance volontaire et maîtrisée dans le signal. Celle-ci rendra possible la détection et correction éventuelle des erreurs de transmission. On parle alors de codage de canal ; citons par exemple les codes de Hamming et Reed Solomon.
Enfin, afin d’être adapté au support de transmission (câble coaxial, fibre optique etc…) le signal est mis en forme par le codage de ligne, opération qui consiste à représenter les différents symboles de l’alphabet (1 et 0 dans le cas d’un alphabet binaire) par des tensions logiques. Citons par exemple les code NRZ, Manchester et Miller. Le choix d’un de ces codes est dicté généralement par des considérations d’encombrement spectral (atténuation de la ligne aux hautes fréquences, impossibilité de passer du continu) et de récupération du rythme de l’horloge de transmission.
Après cette mise en forme du signal, arrive un filtrage permettant l’adaptation au support de transmission ; on retrouve également un filtre à l’entrée du récepteur. Les caractéristiques de ces deux filtres sont primordiales pour les performances de la transmission, en particulier en ce qui concerne le taux d’erreur.
C’est à ces filtres que nous allons nous intéresser au cours de cette séance. Les remarques suivantes permettent de justifier leur présence dans un premier temps :
- la bande passante disponible sur le canal n’est pas illimitée, soit parce que celui-ci introduit une atténuation, soit parce qu’un nombre d’utilisateurs important, limite la place attribuée à chacun ;
- le canal introduit un bruit qui vient se superposer au signal utile ; il faudra atténuer ce bruit à la réception.
Pour mener cette étude nous décomposerons le problème en deux cas de figure, en considérant dans un premier temps un canal non bruité mais limité en fréquence, puis en considérant un canal bruité illimité en fréquence.
Enfin nous ferons la synthèse de ces deux cas pour obtenir la situation réelle.
Nous limiterons notre étude à une transmission binaire (deux symboles possibles), mais les résultats peuvent être étendus à une transmission quelconque.
1. Cas d’un canal non bruité de bande passante réduite
La partie qui nous intéresse peut être alors modélisée par le schéma ci-après :
Nous supposons ici que l’atténuation introduite l’est volontairement par un filtre placé en sortie de l’émetteur afin de permettre l’utilisation du support par plusieurs utilisateurs.
Le problème reste le même si on considère en plus une atténuation C(f) introduite par le canal et un filtre éventuel GR(f) en entrée du récepteur, il suffit alors de remplacer GE(f) par GE(f).C(f).GR(f).
1.1. Aspect fréquentiel
Les travaux de Shanon et Nyquist concernant la théorie de la transmission d’information nous indiquent que pour transmettre un débit de symbole TS (nombre de symboles transmis par secondes en Baud, c’est à dire le débit numérique en bits/s dans le cas d’une transmission binaire –2 symboles +/-5 V par exemple-) il faut disposer d’une bande passante au moins égale à 1/(2.TS).
Le programme suivant sous Scilab permet d’illustrer cet énoncé, dans le domaine fréquentiel dans un premier temps.
Un signal binaire aléatoire « se » est généré avant d’être sur échantillonné afin d’obtenir un signal NRZ. Celui-ci est ensuite filtré par un filtre passe bas d’ordre 4. Les densités spectrales de puissance ou DSP des signaux NRZ avant et après filtrage, ainsi que la réponse fréquentielle du filtre sont affichées.
clear
//
// définition des constantes
// période d’un symbole, coefficient de sur échantillonnage, fréquence de
coupure du filtre
Ts=1e-3; Sech=16 ; fc=800 ;
// période d’échantillonnage, nombre de bits, nombre de points
Te=Ts/Sech ;
Nbit=256 ;Nmax=Nbit*Sech ;
//
// définition du vecteur temps
t=Te*(0: Nmax-1);
//
// signal aléatoire, puis sur échantillonnage pour obtenir un signal NRZ
se=sign(rand(1,Nbit,'n'));
se_sur=(matrix(ones(Sech,1)*se,1,Nmax)) ;
//
// élaboration d’un filtre analogique de Chebycheff, d’ordre 4,
d’ondulation 0,1
// de fréquence de coupure 800 Hz
Ge=analpf(4,'cheb1',[.1 0],2*%pi*fc);
//
// préparation du tracé de la réponse fréquentielle du filtre
f=1/Te/Nmax*(1:Nmax);
gain=freq(Ge(2),Ge(3),%i*2*%pi*f);
//
// calcul des DSP du signal NRZ et signal NRZ filtré
DSPe=(1/Nmax*abs(fft(se_sur,-1)))^2;
DSPr=DSPe.*abs(gain).^2;
//
// troncature de grandeurs à afficher pour effet zoom
f_aff=f(.11/16*Nmax:Nmax/4);
gain_aff=abs(gain(.11/16*Nmax:Nmax/4));
DSPe_aff=DSPe(.11/16*Nmax:Nmax/4);
DSPr_aff=DSPr(.11/16*Nmax:Nmax/4);
//
//affichage fréquentiel
xset("window",0)
; xbasc(0); xset("font size",4); xset("thickness",2);
xsetech([0,0,1,.3]);
plot2d(f_aff,
10*log10(DSPe_aff+%eps),logflag="ln",rect=[1e2,-180,1e4,20],nax=[1,2,2,5]);
xtitle("DSP du signal
transmis","f(Hz)","DSP");
xsetech([0,1/3,1,.3]);
plot2d(f_aff,20*log10(gain_aff),logflag="ln",
rect=[1e2,-70,1e4,10],nax=[1,2,2,4]);
xtitle("gain du filtre","f(Hz)","DSP");
xsetech([0,2/3,1,.3]);
plot2d(f_aff, 10*log10(DSPr_aff+%eps),logflag="ln", rect=[1e2,-180,1e4,20],nax=[1,2,2,5]);
xtitle("DSP du signal reçu","f(Hz)","DSP");
La fonction « analpf » calcule un filtre passe bas analogique en fonction des paramètres précisés, ordre, type, atténuation, fréquence de coupure. Elle renvoie 4 informations, dont 3 vont nous intéresser ici : la fonction de transfert Ge, le numérateur de celle-ci Ge(2) et le dénominateur Ge(3). A l’aide de la fonction « freq » on peut alors calculer différents points de Ge, en précisant dans l’ordre : numérateur, dénominateur et un vecteur ligne donnant les valeurs souhaitées.
L’affichage est fait pour des fréquences allant de 100 Hz à 4 kHz. Pour cela nous avons tronqué, aux échantillons souhaités les vecteurs à afficher. Cette astuce évite de faire la troncature avec l'instruction « rect » qui fonctionne correctement sous Unix, mais reste très aléatoire sous Windows.
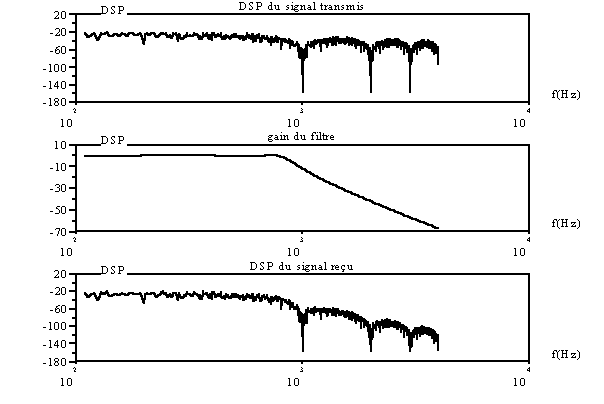
Comme on peut le voir sur l’affichage suivant, l’intégralité du spectre du signal NRZ émis ne passe pas le filtre.
Voyons maintenant ce qui se passe si on s’approche de la limite fixée par Shanon et Nyquist.
Voici le même cas de figure, mais cette fois avec une fréquence de coupure à 500 Hz pour le filtre, ce qui correspond théoriquement à la limite extrême, même si le filtre que nous utilisons n’a pas une coupure parfaitement raide.
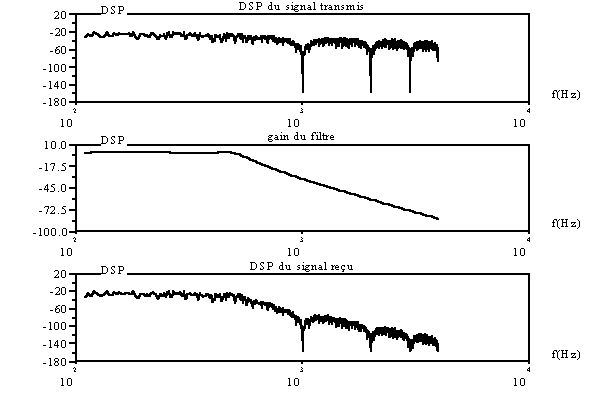
On peut noter cette fois que même le lobe principal de la DSP n'est pas entièrement transmis.
1.2. Aspect temporel
Pour faire l'étude dans le domaine temporelle, on effectue cette fois le filtrage avec la transformée de Fourier, ce qui nous permettra de conserver la phase du signal (contrairement à la DSP) et ainsi de retrouver l'expression du signal filtré par transformée inverse. Avant de faire le calcul de la transformée inverse, on « symétrisera » le spectre du signal filtré afin d’obtenir une partie réelle paire et une partie imaginaire impaire, caractéristique des signaux réels (revoir la séance de présentation de Scilab).
// calcul de la fft et filtrage
Se_sur=1/Nmax*fft(se_sur,-1) ;
Sr=Se_sur .* gain ;
//
// calcul de la fft inverse en respectant les symétrie
Sr=[Sr(1 :Nmax/2),
conj(Sr(Nmax/2+1 : -1 : 2))];
sr= Nmax*fft(Sr, 1) ;
//
// affichage
xset("window",1)
; xbasc(); xset("font size",4) ; xset("thickness",2) ;
//
xsetech([0,0,1,1/3]);plot2d3((1:length(se)),se,rect=[0,-1.5,
Nbit+1,1.5]);
xtitle("information émise","rang", "amplitude
(V)");
//
xsetech([0,1/3,1,1/3]);plot2d(t, se_sur, rect=[0, -1.5, Nmax*Te, 1.5]);
xtitle("signal émis","temps (s)", "amplitude
(V)");
//
xsetech([0,2/3,1,1/3]);plot2d(t,sr, rect=[0, -1.5, Nmax*Te, 1.5]) ;
xtitle("signal reçu","temps (s)", "amplitude
(V)");
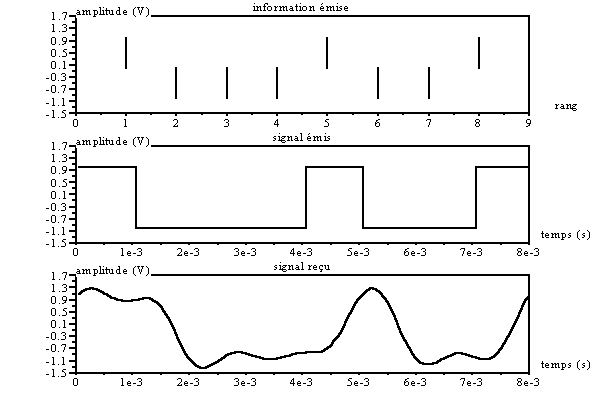
Voici les chronogrammes
obtenus :
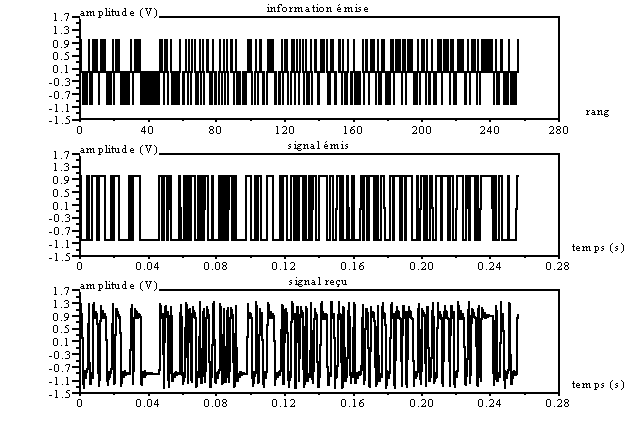
Une dilatation d’échelle
permet une meilleur approche des phénomènes :
// troncature des signaux
se2=se(1:8);
se_sur2=se_sur(1:8*Sech);
sr2=sr(1:8*Sech);
t2=t(1:8*Sech);
//
// affichage
xset("window",2)
; xbasc(2) ; xset("font size",4) ; xset("thickness",2);
//
xsetech([0,0,1,1/3]);plot2d3((1:length(se2)),se2,rect=[0,-1.5,8+1,1.5]);
xtitle("information émise","rang", "amplitude
(V)");
//
xsetech([0,1/3,1,1/3]);plot2d2(t2,se_sur2, rect=[0, -1.5, 8*Sech*Te,
1.5]);
xtitle("signal émis","temps (s)", "amplitude
(V)");
//
xtitle("signal reçu","temps (s)", "amplitude
(V)");
Observons les mêmes chronogrammes, mais avec une bande passante du 500 Hz pour le filtre :
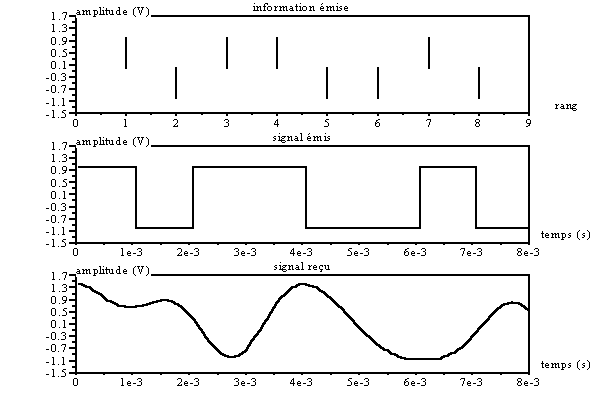
On remarque que cette fois les différents niveaux logiques vont être plus difficiles à différentier (surtout lorsque l’on ajoutera du bruit sur le canal).
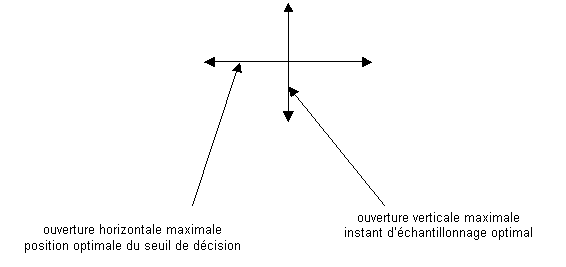
Cette représentation n’est cependant pas très adaptée à ce que nous souhaitons mettre en évidence, aussi préfère t-on souvent utiliser un diagramme dit de l’œil, à cause de sa ressemblance avec un œil humain entrouvert.
1.3. Diagramme de l’œil
Pour obtenir un tel diagramme, il suffit d’observer le signal reçu à l’oscilloscope à mémoire, en synchronisant la base de temps sur l’horloge de l’émetteur. La base de temps est réglée de manière à permettre l’affichage d’une ou deux fois la durée d’un symbole à l’écran. On fait ensuite l’acquisition du plus grand nombre de traces possible, qui viennent se superposer à l’écran.
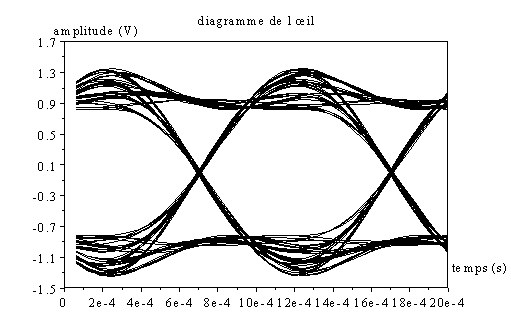
On obtiendrait alors dans le cas de notre filtre à 800 Hz pour un débit de symbole de 1 kHz, le chronogramme suivant :
La matrice du signal est ensuite mise en forme, de manière à présenter des colonnes de hauteur correspondant à 2 périodes de symbole, soit 2.Sech ; on visualisera ainsi le diagramme de l’œil sur 2.Ts.
La matrice temps est ensuite constituée d'une matrice dont le nombre de colonne correspond à la durée de deux symboles et le nombre de ligne au nombre de symboles divisé par 2.
Le style d’affichage doit être identique pour toutes les courbes, « style » sera donc une matrice ligne de 1 (si ce nombre est positif, le tracé est continu et la couleur dépend de la valeur ; s’il est négatif, le tracé est fait de petits symboles fonction de la valeur absolue).
// Diagramme de l’œil
//
// mise en forme de la matrice du signal
s_oeil=matrix(sr,2*Sech,Nbit/2);
//
// mise en forme de la matrice du temps
t_oeil=Te*(1:2*Sech)' *ones(1,Nbit/2);
//
// mise en place des styles, tous identiques
style=ones(1,Nbit/2);
//
//
// affichage
xset("window",3)
; xbasc(3) ; xset("font size",5) ; xset("thickness",1);
plot2d(t_oeil, s_oeil,style,) ;
xtitle("diagramme de l œil","temps (s)",
"amplitude (V)");
1.4. Suppression de l’interférence entre symbole
La difficulté d’interprétation que nous avons constatée précédemment est due au fait qu’un symbole donné a tendance à déborder sur le ou les échantillons suivants. Ce phénomène est connu sous le nom d’interférence entre symboles (IES).
La suppression de l’interférence entre symbole n’impose pas qu’un symbole ne déborde pas sur l’intervalle de temps du symbole voisin : le filtre nécessaire demanderait alors une bande passante infinie (sa réponse impulsionnelle étant finie), ce qui est contraire aux possibilités technologiquesi.
La valeur qui nous intéresse dans un symbole reçu est en fait uniquement la valeur temporelle au moment de la prise de décision ; il suffit alors que la réponse du filtre d’émission aux symboles émis soit nulle à ces instants précis pour supprimer l’interférence entre symbole. Cette manière de voir les choses impose un type de filtre par type de symboles émis, donc par type de codage (NRZ, Manchester etc…).
Afin de simplifier le raisonnement et pour plus de généralité, on peut considérer que l’émetteur envoie à la période TS de débit de symbole, une suite de valeur +/-1, représentée par des impulsions de Dirac. Ces impulsions passent ensuite dans un filtre SE(f), dont la réponse forme le symbole souhaité (suivant le codage NRZ, Manchester etc…), le tout passant ensuite dans un filtre d’émission GE(f).
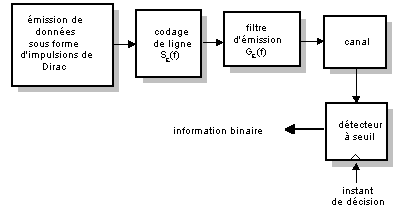
C’est sur la réponse impulsionnelle de ces deux filtres en cascade SE(f).GE(f)=G’E(f) que nous allons maintenant travailler.
Le problème consiste donc à trouver des filtres dont la réponse impulsionnelle s’annule à tous les instants nTS sauf pour n=0, qui représentera l’instant d’échantillonnage (ou de prise de décision).
Ce critère est appelé critère de Nyquist et une famille de filtres communément utilisée répondant à ces exigences (ce ne sont pas les seuls) sont les filtres dits en « cosinus surélevés ».
Leurs réponses impulsionnelles est donnée par l’équation suivante :
![]()
et les réponses fréquentielles par :
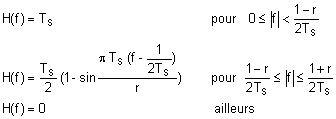
La réponse de ces filtres est paramètrée par un terme « r » dit facteur de « roll-off », facteur d’arrondi ou encore facteur de retombée.
Le programme ci-après permet de tracer la réponse impulsionnelle pour un de ces filtres. Afin de simplifier les écritures, la réponse à été scindée en deux parties. La gestion des valeurs particulières conduisant à des indéterminations est gérée par des tests type « t==0 » qui renvoie comme en langage C la valeur 1 ou 0 suivant que t est nul ou pas. Un développement limité autour de TS/(2r) de h1 permet de montrer que cette fonction tend vers p/4. La condition est exprimée sous forme r.t=TS/2 afin d’éviter la division par 0 lorsque r sera nul dans une utilisation ultérieure.
Ts=1e-3; Sech=16 ;
Te=Ts/Sech; r=.6; Ne=128;
//
// définition du vecteur temps pour 128 échantillons
t=Te*(-Ne/2:Ne/2);
//
// calcul de la réponse impulsionnelle du filtre
h1=cos(%pi*r*t/Ts)./(1-(4*r^2*t.^2)/Ts^2+(abs(r*t)==Ts/2))+(abs(r*t)==Ts/2)*%pi/4;
h2=(sin(%pi*t/Ts))./(%pi*t/Ts+(t==0))+(t==0);
h=h1.*h2;
//
// affichage
xbasc(); xset("font
size",5); xset("thickness",2);
plot2d3(t,h);
xtitle("réponse impulsionnelle pour un filtre en cosinus surélevé;
r=0,6", "temps (s)", "amplitude");
Ce filtre sera synthétisé dans la pratique sous forme numérique, aussi a t-il été représenté de manière discrète. Il est important à ce niveau de ne pas confondre l’échantillonnage nécessaire au filtrage numérique et l’échantillonnage du signal filtré qui permet de savoir si le symbole reçu est un niveau logique 1 ou 0 (dans notre exemple, il y a un rapport 16 entre les deux fréquences).
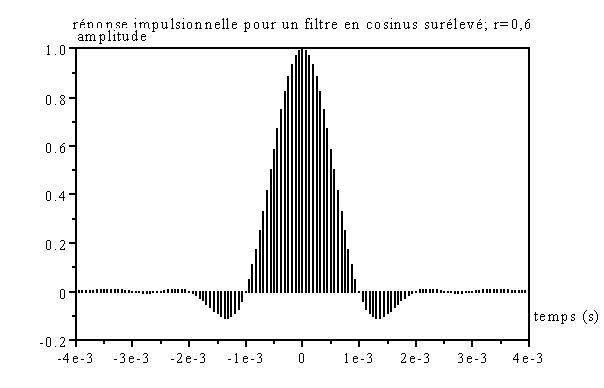
On peut noter que la réponse s’annule bien à chaque multiple de TS (qui vaut ici 1 ms). On notera également que cette réponse n’est pas causale : il suffira alors de la décaler pour obtenir un filtre réalisable physiquement.
La réponse fréquentielle peut être obtenue par la transformée de Fourier de la réponse impulsionnelle ou par l’implantation des expressions données ci-dessus.
// Réponse fréquentielle
clear
//
// définition des constantes
Ts=1e-3; Nbpt=4096; pas=1/Ts/Nbpt; r=.6;
//
// définition du vecteur fréquence
f=pas*(1:Nbpt);
//
// calcul par zones de la réponse
z1=Ts*ones(1,Nbpt*(1-r)/2 -1);
z2=Ts/2*(1-(sin(%pi*Ts*(f-1/2/Ts)/(r+(r==0)))));
z22=z2(Nbpt*(1-r)/2:Nbpt*(1+r)/2);
z3=zeros(1,
Nbpt*(1-(1+r)/2)+1) ;
//
// affichage
xbasc(); xset("font
size",5); xset("thickness",2);
plot2d(f,H(1:Nbpt))
xtitle("réponse fréquentielle du filtre en cosinus surélevé pour
r=0,6 et Ts=1 ms","fréquence (Hz)");

Observons maintenant l’influence du facteur d’arrondi. Pour tracer différentes réponses, on peut utiliser le programme suivant, dans lequel le facteur r est devenu une matrice colonne contenant les valeurs souhaitées du coefficient d’arrondi :
// Réponses impulsionnelles paramètrées par r
clear
//
// définition des constantes
Ts=1e-3; Sech=16 ;
Te=Ts/Sech; r=(0:.5:1)'; Nbit=256 ; Ne=128 ;
//
// vecteur temps
t=Te*(-Ne/2: Ne/2);
//
// calcul des réponses
h1=cos(%pi*r*t/Ts)./(1-(4*r^2*t.^2)/Ts^2+(abs(r*t)==Ts/2))+(abs(r*t)==Ts/2)*%pi/4;
h2a=(sin(%pi*t/Ts))./(%pi*t/Ts+(t==0))+(t==0);
h2=ones(3,1)*h2a;
h=h1.*h2;
//
// affichage
h_aff=h';
t_aff=t'*ones(1,3);
xbasc(); xset("font
size",4); xset("thickness",2);
plot2d(t_aff,h_aff,style);
xtitle("réponse impulsionnelle des filtres en cosinus surélevé
paramétrés en r");
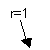
![]()
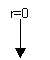

On observe de nouveau l’annulation des réponses à chaque multiple de la période d’émission de symbole.
On notera également que plus le facteur d’arrondis est proche de l’unité, plus le filtre est aisé à synthétiser numériquement : sa réponse tendant plus rapidement vers 0, le nombre d’échantillons nécessaire à la synthèse sera alors plus faible. En contre partie sa réponse fréquentielle sera moins raide, nécessitant une bande passante plus élevée pour la transmission.
A l’autre extrémité, avec comme valeur limite r=0, on obtient une fonction porte pour la réponse fréquentielle d’un filtre passe bas idéal. Ce cas de figure est bien entendu impossible à obtenir, la moindre troncature de la réponse impulsionnelle adoucissant la pente de la réponse fréquentielle.
Les réponses fréquentielles en fonction de r sont données ci-après :
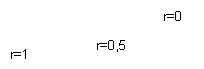
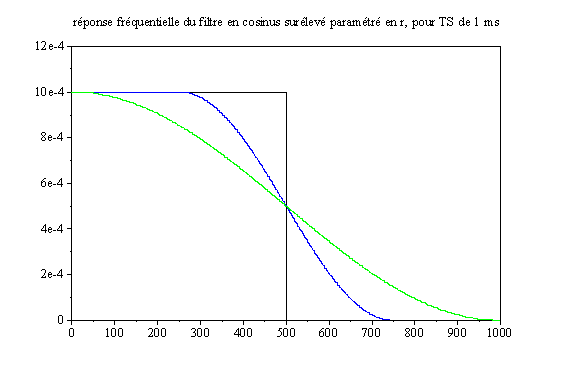
D’une manière générale, le choix d’un facteur d’arrondis faible se paie par une bande passante nécessaire plus élevée comme le montre l’expression de la réponse fréquentielle, où l’on peut voir que la bande nécessaire vaut (1+r)/2TS. Il ne s’agit pas ici de bande passante à –3 dB ou autre critère, toute la bande définie dans la réponse étant nécessaire pour obtenir le résultat escompté.
La valeur du facteur d’arrondi communément retenue est autour de 0,6.
Le programme ci-après permet d’illustrer, dans le cas de la transmission NRZ précédente l’avantage d’un filtre de Nyquist.
// Réponse impulsionnelle du filtre
clear ;
//
// constantes
Ts=1e-3; Sech=8 ;
Nech=64; Te=Ts/Sech;r=.6 ; Nbit=256
//
// vecteur temps
t=Te*(1:4096) ;
//
// réponse impulsionnelle du filtre
Tf=Te*(-Nech/2:(Nech/2-1))
;
h1=cos(%pi*r*Tf/Ts)./(1-(4*r^2*Tf.^2)/Ts^2+(abs(r*Tf)==Ts/2))+(abs(r*Tf)==Ts/2)*%pi/4;
h2=(sin(%pi*Tf/Ts))./(%pi*Tf/Ts+(Tf==0))+(Tf==0);
h=h1.*h2;
//
// affichage de la réponse
xset("window",0)
; xbasc(0); xset("font size",5); xset("thickness",2);
plot2d3((1:length(h)),h);
xtitle("réponse impulsionnelle du filtres pour r=0,6 sur 64 échantillons","rang",
"amplitude");
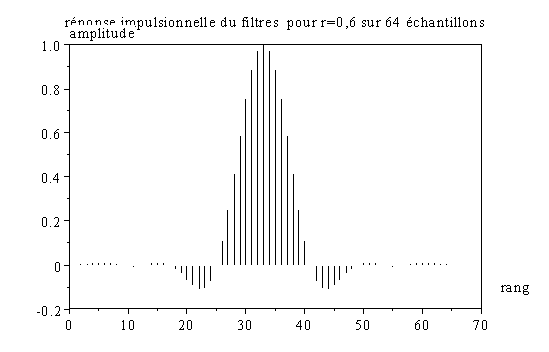
Puis continuons la description de la chaîne de transmission complète . Afin de rester proche d’un système réel, le filtrage est maintenant réalisé directement dans l’espace temporel par convolution à l’aide de la fonction « convol » (même si Scilab effectue le calcul par fft) ; de cette manière on pourra éventuellement juger de l’influence du nombre d’échantillons du filtre. On supprimera alors les échantillons supplémentaires introduit par le produit de convolution.
// Signaux obtenus
//
// signaux binaire et NRZ
se=sign(rand(1,Nbit,'n'));
se_sur=(matrix([1; zeros(Sech-1,1)]*se,1,Sech*Nbit)) ;
//
// signal filtré reçu par le récepteur
sr=convol(h,se_sur);
//
// suppression des échantillons introduit par la convolution
sr_aff=sr(1:length(sr)-Nech+1);
//
// dilatation des échelles d’affichage
se2=se(1:16);
se_sur2=se_sur(1:16*Sech);
sr_aff2=sr_aff(1+Nech/2:16*Sech+Nech/2);
t2=t(1:16*Sech);
//
// affichage
xset("window",1)
; xbasc(1); xset("font size",4); xset("thickness",2);
//
xtitle("information
émise","rang","niveau");
//
xsetech([0,1/3,1,1/3]);plot2d2(t2,se_sur2, rect=[0,-1.5,16e-3,1.5]);
xtitle("signal émis","temps (s)","amplitude
(V)");
//
xsetech([0,2/3,1,1/3]);plot2d(t2,sr_aff2, rect=[0,-1.5,16e-3,1.5]) ;
xtitle("signal reçu","temps (s)", "amplitude
(V)");
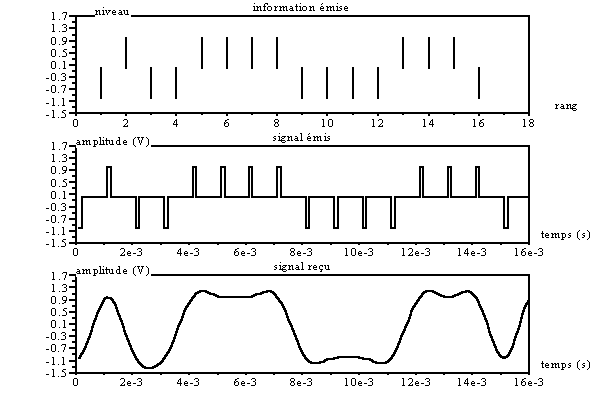
Remarque : le signal codé peut être représenté soit comme nous l’avons fait au début par sur échantillonnage, soit en convoluant les impulsions de Dirac émise avec un filtre dont la réponse impulsionnelle a la forme du symbole de codage :
// Génération du signal NRZ par convolution
//
// réponse impulsionnelle du filtre
h_symb=ones(1,Sech);
//
// convolution
s_symb=convol(se_sur2,h_symb);
//
// affichage
xset("window",2)
; xbasc(2) ; xset("font size",4); xset("thickness",2);
xtitle("information
émise","rang","niveau");
//
xsetech([0,1/2,1,1/2]);
plot2d2(t2,s_symb(1:length(s_symb)-8+1)) ;
xtitle("signal codé", "temps (s)","amplitude
(V)");
Lors de l'affichage du diagramme de l'œil, afin d’éviter de visualiser les transitoires dus au produit de convolution, un nombre d’échantillons égal à Nech la longueur du filtre, sont supprimés, la suppression étant équirépartie en fin et début du signal. Les quatre derniers échantillons sont également supprimés, car ils faussent le diagramme de l’œil. D'autre part, le temps a été remplacé sur l'axe des abscisses par le rang de l'échantillon.
// Diagramme de l’œil
//
// suppression des effets de bord
sr_rec=sr(1+Nech/2:length(sr)-Nech/2+1-2*Sech);
//
// mise en forme de la matrice
s_oeil=matrix(sr_rec,2*Sech,Nbit/2-1);
//
// matrice du temps de du style
t_oeil=(1:2*Sech)'*ones(1,Nbit/2-1);
style=ones(1,Nbit/2-1);
//
// affichage
xset("window",3)
;xbasc(3); xset("font size",4); xset("thickness",2);
plot2d(t_oeil, s_oeil,style);xtitle("diagramme de l oeil");
Voici le résultat obtenu pour r=0,6 :
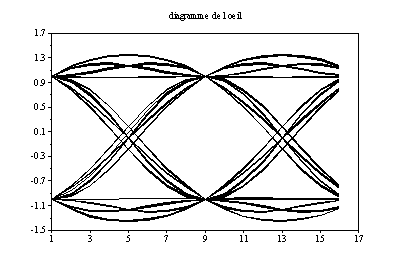
On remarque bien qu’aux instants d’échantillonnage tous les signaux reçus passent par un point particulier, suivant qu’ils transportent un bit à 1 ou 0. On peut noter également que l’instant d’échantillonnage idéal ne correspond pas forcément au maxima ou au minima du signal reçu.
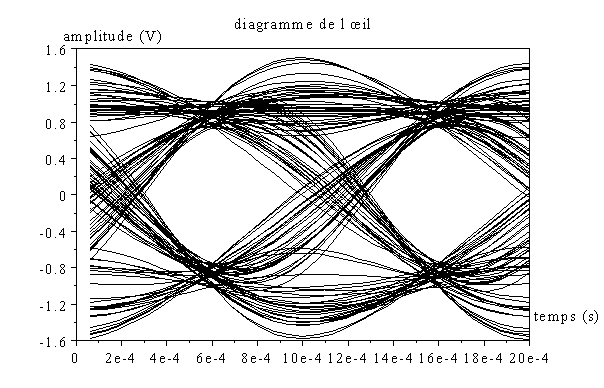
Observons maintenant ce que nous obtenons suivant le facteur d’arrondi.
Diagramme obtenu pour r=1 :

Diagramme pour r=0 (et 128 échantillons pour le filtre) :
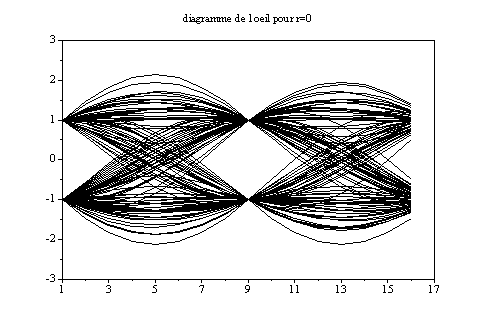
Dans tous les cas de figure, l’IES est nulle au moment de la décision. L’œil est cependant plus ouvert si le facteur d’arrondis est grand, mais la bande passante nécessaire est plus importante.
2. Cas d’un canal bruité de bande passante infinie
L’émetteur envoie directement cette fois les signaux codés (NRZ, Manchester etc…) sur le canal qui les transmet en y ajoutant du bruit. Le signal reçu va donc être filtré de manière à supprimer au moins le bruit en dehors de la bande utile. Un filtre trop large laissera passer trop de bruit, un filtre trop étroit dégradera l’allure du signal utile (et introduira de l’interférence entre symbole).
Est-il possible d’optimiser le rapport signal sur bruit en choisissant judicieusement la réponse du filtre GR(f) ?
La réponse à cette question peut être apportée de plusieurs manières :
En calculant le rapport signal sur bruit en sortie du filtre et en déterminant alors l’expression du filtre de manière à maximiser le rapport. On trouvera les détails de ce calcul dans les trois premières références citées en bibliographie.
On peut approcher le résultat par un raisonnement qualitatif dans le domaine fréquentiel : lorsque le signal émis est un symbole se(t) de transformée de Fourier SE(f), la transformée de Fourier en sortie du filtre a pour expression :
SR(f)=GR(f).[SE(f) + B0]
Le terme B0 est censé représenter la transformation de Fourier du bruit, constante sur tout le spectre (il faudrait parler de DSP, mais ce n’est ici qu’un raisonnement qualitatif).
Si on donne à GR(f) l’expression S*E(f), on maximalise le premier terme sans trop augmenter le second. On obtient alors :
SR(f)=II SE(f) II2 +S*E(f).B0
On a ainsi donné à GR(f) le même module que celui de l’impulsion reçue de manière à donner beaucoup de gain là où il y avait beaucoup de signal utile et peu là où le bruit était prédominant.
La réponse impulsionnelle d’un tel filtre est :
gr(t)=se(-t)
(la transformée de Fourier de f(at) est F(j.f/a)/IaI).
Cette réponse n’étant pas causale, on rajoute un décalage temporel comme nous l’avions fait pour les filtres de Nyquist, et éventuellement un gain constant. On arrive alors à :
gr(t)=K.se(t0-t)
Il est également possible de raisonner sur la corrélation. Nous avons vu lors de la séance précédente que pour retrouver un signal sinusoïdal noyé dans du bruit, un moyen simple consistait à faire une autocorrélation. On améliorait encore la détection en faisant une corrélation avec une sinusoïde de même fréquence. D’une manière générale, si on connaît la forme du signal attendu, une corrélation par cette forme permet l’extraction. Nous avions également vu que corréler deux signaux x(t) et y(t) était équivalent à faire la convolution x*(-t) * y(t). La corrélation devient donc équivalente à filtrer par un quadripôle dont la réponse impulsionnelle est se(-t) si se(t) est le signal attendu.
Le filtre adapté
(matched filter) à un symbole émis se(t)
a donc pour réponse impulsionnelle Kse(t0-t).
K est une constante quelconque et t0 un temps supérieur ou égale à la durée du symbole de manière à rendre le filtre causal.
Dans le cas d’une transmission binaire, deux symboles sont émis de manière aléatoire (que l’on supposera équiprobable), un symbole s1(t) pour le niveau logique 1 et un symbole s0(t) pour le niveau logique 0. On montre que la réponse impulsionnelle du filtre adapté est alors de la forme :
K.[s1(t0-t)-s0(t0-t)].
// Réponse à une impulsion et à un symbole du filtre adapté
clear;
//
// constantes, débit, facteur de sur échantillonnage, période
d’échantillonnage
// nombres de bits émis, nombre de points
// rapport signal sur bruit, constante du temps du filtre adapté
Ts=1e-3; Sech=16 ; Te=Ts/Sech;
Nbit=2; Nbpt=Nbit*Sech;
SB=100; t0=3*Ts/2;
//
// vecteurs temps
t=Te*(1:Nbpt);
//
// donnée 1 suivie de 0, puis signal NRZ correspondant
se=[1 0];
se_sur=(matrix(ones(Sech,1)*se,1,Nbpt)) ;
//
// réponse du filtre adapté
gr=[zeros(1,(-Ts+t0)/Te),ones(1,Ts/Te)];
//
// signal en sortie du filtre
sf=convol(gr,se_sur);
//
// adaptation du temps pour l’affichage complet du signal filtré
tsf=Te*(1:length(sf));
//
// affichage
xbasc(); xset("font
size",4); xset("thickness",2);
//
xsetech([0,0,1,1/3]); plot2d(t,se_sur,rect=[0,0,2e-3,1.5]);
xtitle("signal émis"," temps",
"amplitude");
//
xsetech([0,1/3,1,1/3]);plot2d([1:length(gr)],gr,rect=[0,0,2*Sech,1.5]);
xtitle("réponse impultionnelle du filtre","rang",
"amplitude");
//
xsetech([0,2/3,1,1/3]);
plot2d(tsf,sf);
xtitle("réponse du filtre au signal émis","temps",
"amplitude");
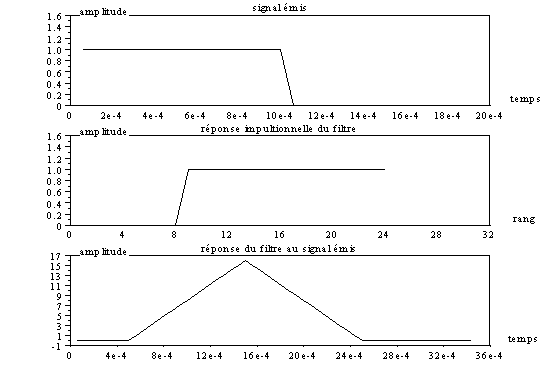
On remarque que la réponse du filtre à un symbole présente un maximum pour t0 ; c’est donc à cet instant qu’il faudra échantillonner le signal pour prendre une décision sur sa valeur.
Observons maintenant ce qui se passe pour une suite de symboles, faiblement bruités (rapport signal sur bruit de 100) dans un premier temps.
// Réponse d’une chaîne complète avec filtre adapté
//
clear;
//
// constantes
Ts=1e-3; Sech=8 ; Te=Ts/Sech; Nbit=16; Nbpt=Nbit*Sech;
t=Te*(1:Nbpt);SB=100; t0=3*Ts/2;
//
// données et signal NRZ correspondant
se=sign(rand(1,Nbit,'n'))
se_sur=(matrix(ones(Sech,1)*se,1,Nbpt)) ;
//
// signal fictif permettant de repérer les instants idéaux
d’échantillonnage et les valeurs attendues
// suréchantillonnage par des 0 du signal de donnée
se_surd=(matrix([1; zeros(Sech-1,1)]*se,1,Nbpt)) ;
//
// synchronisation avec les maxima et minima de la réponse et troncature
pour l’affichage
ck=3*[zeros(1,t0/Te-1),se_surd]; ck=ck(1: Nbpt);
//
// génération du bruit
b=sqrt(1/SB)*rand(1,Nbpt,'n');
//
//
// ajout du bruit au signal utile
sr=se_sur+b;
//
// réponse du filtre
gr=[zeros(1,(-Ts+t0)/Te),ones(1,Ts/Te)];
//
// filtrage et troncature pour l’affichage
sf=convol(gr,sr); sf=sf(1: Nbpt);
//
// extraction du signe de la valeur au moment de l’échantillonnage, donc
du niveau logique.
sortie=sign(sf.*abs(ck)) ;
//
// mise sous forme NRZ par convolution de la valeur et troncature pour
affichage
s_basc=convol(ones(1,Sech), sortie); s_basc=s_basc(1:Nbpt);
//
// affichage
xbasc(); xset("font size",3);
xset("thickness",2);
//
xsetech([0,0,1,1/4]);plot2d3((1:length(se)),se,rect=[0,-1.5,Nbit+1,1.5]);
xtitle("information émise");
//
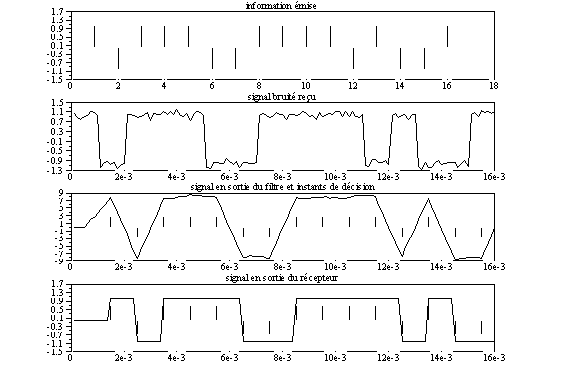
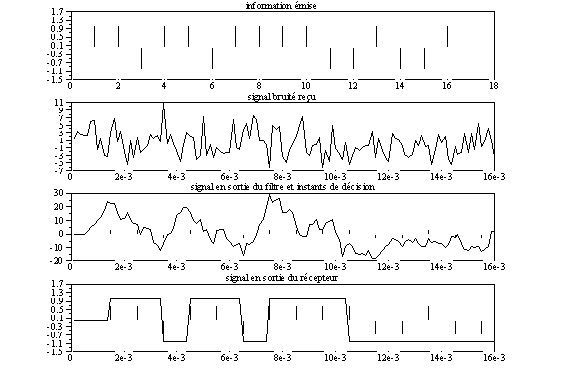
xsetech([0,1/4,1,1/4]);plot2d(t,sr); xtitle("signal bruité
reçu");
//
xsetech([0,2/4,1,1/4]);plot2d(t,sf);xtitle("signal en sortie du
filtre et instants de décision");
xsetech([0,2/4,1,1/4]);plot2d3(t,ck/2);
//
xsetech([0,3/4,1,1/4]);plot2d3(t,ck/8,rect=[0,-1.5,16e-3,1.5]);
//
xsetech([0,3/4,1,1/4]);plot2d(t,s_basc);xtitle("signal en sortie du
récepteur");
Voici maintenant les chronogrammes obtenus pour un rapport signal sur bruit de 0,1
3. Cas d’un canal réel
4. Etude d’un cas pratique
Bibliographie
Communications numériques par A. Glavieux et M. Joindot chez Masson
Signal et communication numérique par J.M. Brossier chez Hermes
Transmission des signaux numériques par H. Sari Techniques de l’ingénieur E7100
Premier pas en communications numériques par C. Bazile et A. Duverdier
sur http://www-rocq.inria.fr/scilab