Traitement du signal avec Scilab :
convolution et approche du filtrage numérique
Sommaire
3 Application à la réalisation d’un filtre numérique
3.1 Approche de la transformation en z
3.2 Tracé de la réponse fréquentielle
Annexe 1 : programmes des illustrations
___________________________________________________________________
Alors qu’elle intervient peu dans le traitement du signal analogique où on a recours à la transformation de Fourier pour éviter son utilisation, la convolution joue un rôle important dans le traitement numérique du signal, en particuliers pour la réalisation de filtres numériques.
L’objectif de cette séance est de se familiariser avec cette opération, en commençant par une approche intuitive, puis en passant à une application sur la synthèse d’un filtre numérique. Nous profiterons de la dernière partie pour effectuer une approche rapide de la transformée en z, cette notion étant très liée aux réponses impulsionnelles, donc au produit de convolution.
1 Approche intuitive
Un signal analogique peut être vu comme une suite d’impulsions de largeur Dt, suffisamment faible pour que l’amplitude reste constante. Connaissant la réponse h(t) d’un quadripôle linéaire à une impulsion unitaire, en appliquant le théorème de superposition, on peut retrouver la réponse du quadripôle à n’importe quel signal. Il suffira de simplement calculer la somme des réponses à chaque impulsion élémentaire.
Les figures suivantes représentent dans le cas d’un système du premier ordre, de pulsation propre w0 dont la réponse impulsionnelle est de la forme w0e-w0t. Dans un premier temps, l’étude se fait avec des grandeurs discrètes, qui se prête bien à une approche qualitative.
On observe sur les figures de gauche une impulsion en n=0 et en dessous sa réponse h(n). Sur les figures de droites, on retrouve la même impulsion en n=k, ainsi que la réponse associée h(n-k).
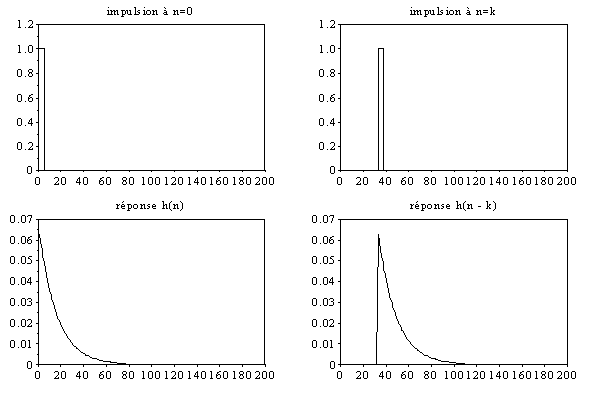
Sur les figures suivantes, on a représenté une fonction porte, découpée en impulsions élémentaires et en dessous la réponse à chaque impulsion élémentaire. On effectue ensuite la somme de ces réponses.

La forme de la réponse obtenue est bien celle attendu pour un premier ordre. On constate cependant une ondulation importante, ainsi qu’une valeur asymptotique qui n’est pas unitaire lors de la montée. Ces deux défauts sont dus au choix d’une largeur d’impulsion trop grande par rapport au pas d’échantillonnage, choix justifié par la nécessité de mettre en évidence le phénomène.
Le programme Scilab permettant le calcul est fourni en annexe, et pourra être utilisé pour tester des options différentes.
2 Expression mathématique
Considérons maintenant un système échantillonné à la période TE. Le pas d’échantillonnage correspond alors à la largeur d’une impulsion élémentaire.
D’après ce qui précède, montrer que si h(n) est la
réponse impulsionnelle d’un quadripôle, la réponse de ce quadripôle à une
entrée VE(n)
sera :
![]()
Quelle propriété de h(n) nous permet d’écrire :
![]()
Remarque : l’étude faite ici considère des signaux numériques sans énergie ; pour fournir de l’énergie aux signaux, il aurait fallu introduire un coefficient TE en facteur dans la sommation ; ce facteur est classiquement introduit pour effectuer ce genre de démonstration. Celle ci gagne alors en rigueur mais est moins représentative des systèmes numériques modernes.
En déduire que pour un signal analogique pour lequel TE tend vers 0,
on a :
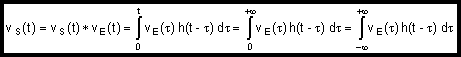
Le dernier terme de l’égalité peut être écrit si on considère que vE(t) est un signal causal (nul pour les temps négatifs).
Les principales propriétés du produit de convolution sont :
- la commutativité
- l’associativité
- la distributivité pour l’addition
- accepter la distribution de Dirac d(t) est l’élément neutre
- devenir un produit classique par transformation de Fourier (ou transformation inverse)
- être la transformée de Fourier (ou la transformée inverse) du produit classique.
3 Application à la réalisation d’un filtre numérique
Une méthode simple utilisée pour la synthèse d’un filtre numérique, consiste à échantillonner la réponse impulsionnelle hA(t) du filtre analogique équivalent pour obtenir les coefficients hE(n) de la réponse indicielle du filtre numérique. Cette méthode est appelée méthode de la fenêtre (la réponse impulsionnelle étant « fenêtrée » avant d’être échantillonnée).
En appelant {hE(n)} la suite de coefficient hE(n) de la réponse impulsionnelles du filtre numérique, on obtient alors :
![]() et
et ![]()
où Ne représente le nombre de coefficients de la réponse impulsionnelle du filtre et TE la période d’échantillonnage.
La présence du terme TE en facteur est justifiée de la manière suivante : l’échantillonnage de la réponse impulsionnelle est équivalent à une multiplication par un peigne de Dirac temporelle d’amplitude unitaire et de période TE ; la réponse temporelle du signal est donc convoluée avec la transformée de Fourier de ce signal, soit par un peigne de Dirac d’amplitude 1/TE et de période (fréquentielle) 1/TE. Pour compenser l’atténuation ainsi introduite, il convient donc de multiplier par la réponse impulsionnelle par TE.
Le choix de la réponse du filtre est ici très discutable, les méthodes numériques permettant des performances nettement meilleures. Notre objectif est cependant simplement d’illustrer l’utilisation du produit de convolution et non de réaliser un filtre performant.
Le programme suivant permet de tester cette réponse à deux entrées types. Toutes les constantes sont dans un premier temps définies, puis la réponse du filtre, les entrées et enfin les sorties sont calculées avec la fonction « convol(h,e) » qui réalise la convolution des deux arguments fournis en renvoyant un vecteur résultat sur Nh+Ne-1 échantillons si Nh et Ne sont respectivement le nombre d’échantillons de h et e.
La méthode utilisée par Scilab pour effectuer cette opération consiste en fait à faire le produit des transformées de Fourier des deux signaux, puis calculer la transformée inverse.
clear ;
//
// définition de la fréquence d'échantillonnage, du nombre de points de
calcul,
// du nombre d'échantillons du filtre, des vecteurs temps et
échantillons
Fe=2 ; Te=1/Fe; N=300 ; Ne=50;
t=1/Fe*[0:N-1];n=[0:Ne-1];
//
// définition de la réponse impulsionnelle du filtre
f0=.02 ;
w0=2*%pi*f0 ;
h=1/Fe*w0*exp(-w0*Te*n);
//
// définition des entrées
e1=ones(1,N);
e2=10*sin(w0*t);
//
// calcul des sorties et ajustement du nombre de points
s1=convol(e1,h);
s1=s1(1:N);
s2=convol(e2,h);
s2=s2(1:N);
//
// affichage sur la
fenêtre 0
xset("window",0);xbasc(0);
xset("font size",4);
xsetech([0 ,1/3,1,1/3]) ;plot2d(t,e1) ; ;plot2d(t,s1) ;
xtitle("réponse à un échelon");
xsetech([0 ,2/3,1,1/3]) ; ;plot2d(t,e2) ; ;plot2d(t,s2) ;
xtitle("réponse sinusoïdale à la fréquence de coupure");
xsetech([0
,0,1,1/3]) ;plot2d3(n,h, rect=[-1,0,Ne,w0/Fe]);
xtitle("réponse impulsionnelle");
Ci après sont affichées la réponse impulsionnelle, la réponse à un échelon et à une sinusoïde de fréquence égale à la fréquence de coupure. On retrouve bien les résultats attendus pour ces réponses.

On pourra vérifier d’autre type d’entrées (carré, impulsionnelle, somme de sinusoïdes etc…). On pourra également vérifier que l’on obtient bien le même résultat en utilisant l’algorithme de convolution proposé en annexe pour générer les exemples de la première partie.
3.1
Approche de la
transformation en z
Dans l’exemple du filtre précédent, en supposant afin de simplifier que le filtre n’a que 5 coefficients, donner l’équation récurrente s(n)=f(e(n), e(n-1)…) liant le signal d’entrée « e » au signal de sortie « s ».
Comme on peut le voir, la sortie du filtre obtenu ne dépend que de l’entrée (et pas des valeurs de la sortie aux instants précédents). On parle alors de filtre à réponse impulsionnelle finie (FIR filter) et de filtre non récursif. Ce type de filtre présente l’avantage d’être inconditionnellement stables (pas de rebouclages de la sortie sur l’entrée). Ils présentent cependant des performances moindres que les filtres à réponse impulsionnelle infinie (IIR filter).
Sachant que l’opérateur « z-1 »
traduit un retard d’une période d’échantillonnage, déterminer la fonction de
transfert en z du filtre réalisé.
3.2
Tracé de la
réponse fréquentielle
On souhaite tracer le module de la fonction de transfert de ce filtre en fonction de la fréquence, afin de pouvoir comparer avec le filtre analogique.
D’après la définition de z, quel changement de variable faut-il faire sur la transformée en z pour obtenir la transformée de Fourier de la réponse impulsionnelle échantillonnée du filtre (c’est à dire la fonction de transfert du filtre numérique).
Exécuté à la suite du précédent, le programme ci-après permet de tracer la réponse fréquentielle du filtre. On génère pour cela le polynôme en « z » :à l’aide de la fonction « poly », puis on calcule les valeurs de ce polynôme à l’aide de la fonction « freq ». Ces différentes fonctions ont été détaillées dans la séance d’introduction.
// définition d’un polynôme en z à partir des coefficients de h
H=poly(h,'z','c');
//
// définition de la variation de la pulsation, qui n’a de signification
que pour un intervalle 0 0,5
w=(0:.01:.5);
//
// calcul des valeurs particulières de H
ft=freq(H,1,exp(%i*w));
// affichage sur la fenêtre 1
xset("window",1);xbasc(1);
xset("font size",4);
xsetech([0
,0,1,1/2]) ;plot2d(w,abs(ft));
xtitle("réponse fréquentielle sur échelles linéaires, normalisée en
pulsation");
xsetech([0
,1/2,1,1/2]) ;
plot2d(w(2:length(w)),20*log10(abs(ft(2:length(w)))),
logflag=["ln"]) ;
xtitle("réponse fréquentielle sur échelles semi-log, normalisées en
pulsation");
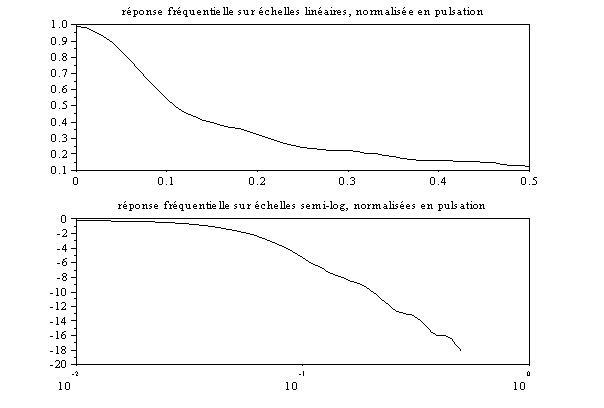
Vérifier sur la figure suivante, que les valeurs des gains statiques et de la pulsation de coupure sont bien celles attendues (attention, sur l’axe des abscisses, la valeur unitaire correspond à la pulsation d’échantillonnage).
On constate cependant la présence d’oscillations (phénomène de Gibbs), dues à la troncature de la réponse temporelle par une fonction porte. Ce phénomène sera détailler lors de l’étude des filtres numériques.
Annexe 1 : programmes des illustrations
clear ;
//
// définition des constantes, nombre de points, nombre d’impulsions
élémentaires
// durée d’une impulsion, nombre d’échantillon sur une réponse
élémentaire
N=200 ; Nrep=30; inc=4; Ne=80 ;
f0=.01 ;
w0=2*%pi*f0 ;
n=[0:Ne-1];
//
// impulsion et réponse impulsionnelle
e0=ones(1,inc) ;
h0=w0*exp(-w0*n);
//
// définition des matrices où seront placé les impulsions et réponse
h=zeros(Nrep, N);
e=zeros(Nrep,N);
//
// initialisation de l’affichage pour la fenêtre 0
xset(“window”,0);
xbasc(0) ; xset(“font size”, 4);
//
// boucle de calcul et d’affichage des impulsions et réponses
for
i=0:inc:inc*Nrep-1,
h(i+1, :
)=[zeros(1,i), h0 ,zeros(1,N-Ne-i)];
e(i+1, :
)=[zeros(1,i), e0 ,zeros(1,N-inc-i)];
xsetech([0
,0,1,1/3]) ;plot2d2((1:N),e(i+1,:), rect=[ 0, 0, N, 1.2]) ;
xsetech([0 ,1/3,1,1/3]) ;plot2d(h(i+1,:)) ;
end
//
// calcul de la sortie
s=sum(h,’r’);
//
// affichage de la sortie et des commentaires
xsetech([0
,2/3,1,1/3]) ;plot2d(s ) ;
xtitle (“somme des réponses élémentaires”);
xsetech([0 ,0,1,1/3]) ; xtitle (“entrée décomposée en impulsions”);
xsetech([0 ,1/3,1,1/3]) ; xtitle (“réponse à chaque impulsion”);
//
// affichage des impulsions et réponses décalées sur la fenêtre 1
xset(“window”,1);
xbasc(1) ; xset(“font size”, 4);
xsetech([0 ,0,1/2,1/2]) ;plot2d2((1 :N),e(1,: ), rect=[ 0, 0,
N, 1.2])
xtitle (“impulsion à n=0”);
xsetech([0
,1/2,1/2,1/2]) ;plot2d(h(1,: )) ;xtitle (“réponse h(n)”);
xsetech([1/2 , 0,1/2,1/2]) ;plot2d2((1 :N),e(33,: ), rect=[ 0,
0, N, 1.2])
xtitle (“impulsion à n=k”);
xsetech([1/2 ,1/2,1/2,1/2]) ;plot2d(h(33,: )) ;xtitle
(“réponse h(n - k)”);